题目内容
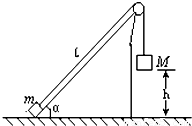
 如图所示为一固定在地面上的楔形木块,质量分别为m和M两个物体,用轻质细绳相连跨过固定在斜面顶端的定滑轮,已知斜面的倾角为α,且M>msinα.用手托住物体M,使之距地面高为h时,物体m恰停在斜面的底端,细绳恰好绷直,并且与斜面的斜边平行,如果突然释放物M,不计一切摩擦.
如图所示为一固定在地面上的楔形木块,质量分别为m和M两个物体,用轻质细绳相连跨过固定在斜面顶端的定滑轮,已知斜面的倾角为α,且M>msinα.用手托住物体M,使之距地面高为h时,物体m恰停在斜面的底端,细绳恰好绷直,并且与斜面的斜边平行,如果突然释放物M,不计一切摩擦.(1)物体M着地时的速度多大?
(2)物体m能沿斜面滑行的最大距离是多少?设斜面足够长.
分析:(1)释放物M到M落地的过程中,M、m组成的系统只有重力做功,机械能守恒,根据机械能守恒定律列式,可求出物体M着地时的速度.
(2)M落地后,m继续沿斜面上升,再根据动能定理求出m上升的距离,即可得到m能沿斜面滑行的最大距离.
(2)M落地后,m继续沿斜面上升,再根据动能定理求出m上升的距离,即可得到m能沿斜面滑行的最大距离.
解答:解:(1)设M落地时的速度为v,系统的机械能守恒得:Mgh-mghsinα=
(m+M)v2
解得,v=
(2)M落地后,m以v为初速度沿斜面匀减速上升,设沿斜面又上升的距离为S,
由动能定理得:-mgSsinα=0-
mv2
物体m能沿斜面滑行的最大距离:L=h+S
①②③式解得:L=
答:
(1)物体M着地时的速度是
.
(2)物体m能沿斜面滑行的最大距离是
.
| 1 |
| 2 |
解得,v=
|
(2)M落地后,m以v为初速度沿斜面匀减速上升,设沿斜面又上升的距离为S,
由动能定理得:-mgSsinα=0-
| 1 |
| 2 |
物体m能沿斜面滑行的最大距离:L=h+S
①②③式解得:L=
| Mh(1+sinα) |
| (M+m)sinα |
答:
(1)物体M着地时的速度是
|
(2)物体m能沿斜面滑行的最大距离是
| Mh(1+sinα) |
| (M+m)sinα |
点评:本题中单个物体机械能不守恒,但二者组成的系统机械能守恒.求m能沿斜面滑行的最大距离时应从斜面底端算起.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
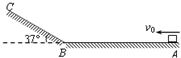 如图所示,一固定在地面上的金属轨道ABC,其中AB长s1=1m,BC与水平面间的夹角为α=37°,一小物块放在A处,小物块与轨道间的动摩擦因数均为μ=0.25,现在给小物块一个水平向左的初速度v0=3m/s.小物块经过B处时无机械能损失(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
如图所示,一固定在地面上的金属轨道ABC,其中AB长s1=1m,BC与水平面间的夹角为α=37°,一小物块放在A处,小物块与轨道间的动摩擦因数均为μ=0.25,现在给小物块一个水平向左的初速度v0=3m/s.小物块经过B处时无机械能损失(sin37°=0.6,cos37°=0.8,g取10m/s2).求: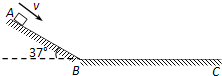 如图所示,一固定在地面上的金属轨道ABC,AB与水平面间的夹角为α=37°,一小物块放在A处(可视为质点),小物块与轨道间的动摩擦因数均为μ=0.25,现在给小物块一个沿斜面向下的初速度v0=1m/s.小物块经过B处时无机械能损失,物块最后停在B点右侧1.8米处(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
如图所示,一固定在地面上的金属轨道ABC,AB与水平面间的夹角为α=37°,一小物块放在A处(可视为质点),小物块与轨道间的动摩擦因数均为μ=0.25,现在给小物块一个沿斜面向下的初速度v0=1m/s.小物块经过B处时无机械能损失,物块最后停在B点右侧1.8米处(sin37°=0.6,cos37°=0.8,g取10m/s2).求: (2006?福建模拟)如图所示,一固定在地面上的光滑斜面的顶端固定有一个轻弹簧,地面上质量为m的物块(可视为质点)向右滑行并冲上斜面,设物块在斜面最低点A的速率为υ,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则物块运动到C点时弹簧的弹性势能为( )
(2006?福建模拟)如图所示,一固定在地面上的光滑斜面的顶端固定有一个轻弹簧,地面上质量为m的物块(可视为质点)向右滑行并冲上斜面,设物块在斜面最低点A的速率为υ,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则物块运动到C点时弹簧的弹性势能为( )