Question

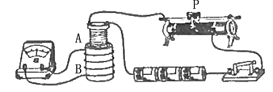
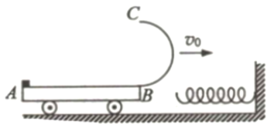
【题目】如图所示，小车右端有一半圆形光滑轨道BC相切车表面于B点，一个质量为m=1.0kg可以视为质点的物块放置在A点，随小车一起以速度=5.0m/s沿光滑水平面上向右匀速运动.劲度系数较大的轻质弹簧固定在右侧竖直挡板上.当小车压缩弹簧到最短时，弹簧自锁(即不再压缩也不恢复形变)，此时，物块恰好在小车的B处，此后物块恰能沿圆弧轨道运动到最高点C.已知小车的质量为M=1.0kg，小车的长度为=0.25m，半圆形轨道半径为R=0.4m，物块与小车间的动摩擦因数为μ=0.2，重力加速度g取10m/s2.求:

(1)物块在小车上滑行时的加速度a；

(2)物块运到B点时的速度；

(3)弹簧在压缩到最短时具有的弹性势能以及弹簧被压缩的距离.

Answer 1

【答案】(1)2m/s2；(2) ；(3)14.5J ； 1m

【解析】

(1)物块在小车上滑行时，由牛顿第二定律

解得

a=2m/s2；

(2)据题，物块恰能沿圆弧轨道运动到最高点C，由重力提供向心力，则有

物块从B运动到C的过程，由机械能守恒定律得

联立解得

(3)根据能量守恒定律得：

解得

Ep=14.5J

从开始接触弹簧到弹簧压缩到最短时，滑块A相对地面的位移

则小车的位移

即弹簧被压缩的距离为0.25m