题目内容
在光滑的水平面上停放着一辆质量为m1的小车，质量为m2的物体与一轻弹簧固定相连，弹簧另一端与小车左端固定连接，将弹簧压缩后用细线将m2拴住，m2静止在小车上的A点，如图10所示.设m2与m1间的动摩擦因数为μ,O点为弹簧原长位置，将细线烧断后，m2、m1开始运动，则：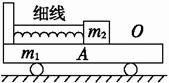
图10
（1）当m2位于O点左侧还是右侧时，物体m2的速度最大？简要说明理由.?
（2）若物体m2达到最大速度v2时，物体m2已相对小车移动了距离s,求此时m1的速度v1和这一过程中弹簧释放的弹性势能Ep.
（3）判断m2与m1最终运动状态是静止、匀速运动还是相对往复运动，并简要说明理由.
解析：(1)m2速度最大的位置应在O左侧.因为细线烧断后，m2在弹簧弹力和滑动摩擦力的合力作用下向右做加速运动，当弹力与摩擦力的合力为零时，m2的速度达到最大，此时弹簧必处于压缩状态.此后，系统的机械能不断减小，不能再达到这一最大速度.?
(2)选m2、m1为一系统，由动量守恒定律得：m2v2=m1v1,又：W克=μm2gs,设这一过程中弹簧释放的弹性势能为Ep,则有Ep=m1v12/2+m2v22/2+W克.由上解得：
v1=m2v2/m1?
(3)m2与m1最终将静止，因为系统动量守恒，且总动量为零，只要m2与m1间有相对运动，就要克服摩擦力做功，不断消耗能量，所以m2与m1最终必定都静止.
练习册系列答案
互动英语系列答案
相关题目
如图所示，在光滑的水平面上停放着一辆平板车，在车上的左端放有一木块B．车左边紧邻一个固定在竖直面内、半径为R的
如图所示，在光滑的水平面上停放着一辆质量为M=2kg的小车，车上的平台是粗糙的，平台长度为s0=3.5m，停在光滑的水平桌面旁．现有一质量为m=l kg的质点C以vo=10m/s的初速度沿水平桌面滑上与桌面等高的平台，然后经A点离开平台，并恰好落在小车平板上的B点．O为A点在平板上的投影点，已知OA=h=5m，OB=s=4m，g取10m/s2，求：
如图所示，在光滑的水平面上停放着一辆质量为M的小车，小车上的平台是粗糙的，停在光滑的水平桌面旁．现有一质量为m的质点C以初速度v0沿水平桌面向右运动，滑上平台后从A端点离开平台，并恰好落在小车的前端B点．此后，质点C与小车以共同的速度运动．已知OA=h，OB=s，则：
如图所示，在光滑的水平面上停放着一辆质量M=6.0kg平板车，在车上左端放有一质量mB=4.0kg木块B．车左边紧邻一个与平板车等高的光滑水平面，现有另一质量 mA=2.0kg的木块A，从左侧光滑水平面上以v0=3.0m/s向右运动，然后与B发生碰撞，设木块A、B碰撞时间很短且为弹性正碰．碰后木块B开始在平板车上滑行，并与固定在平板车上的水平轻质弹簧作用后与弹簧分离，已知木块B把弹簧压缩到最短时距离平板车左侧的距离为L=0.20m，重力加速度为g=10m/s2，木块B与平板车之间的动摩擦因数为μ=0.50．（结果保留两位有效数字）求：
如图所示，在光滑的水平面上停放着小车B，车上左端有一小物体A，A和B之间的接触面前一段光滑，后一段粗糙，且后一段的动摩擦因数μ=0.4，小车长L=2m，A的质量mA=1kg，B的质量mB=4kg．现用l2N的水平力F向左拉动小车，当A到达B的最右端时，两者速度恰好相等，求A和B间光滑部分的长度．（g取10m/s2）