题目内容
7. 如图所示,电荷量为q,质量为m的带电粒子以速度v垂直进入平行板电容器中(不计粒子的重力),已知极板的长度为l,两极板间的距离为d,两极板间的电压为U,试推导带电粒子射出电容器时在偏转电场中的竖直偏转位移y和速度偏转角φ的正切值.
如图所示,电荷量为q,质量为m的带电粒子以速度v垂直进入平行板电容器中(不计粒子的重力),已知极板的长度为l,两极板间的距离为d,两极板间的电压为U,试推导带电粒子射出电容器时在偏转电场中的竖直偏转位移y和速度偏转角φ的正切值.
分析 电子在电场中做抛运动,根据竖直方向匀加速运动的规律和牛顿第二定律,求解竖直偏转位移;
电子飞出电场时的速度可由水平和竖直两个分速度合成,竖直分速度由vy=at求解,从而求解偏转角;
解答 解:电子在电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动,故有:
水平方向:vt=l,可得电子在电场中运动的时间为:t=$\frac{l}{v}$,
竖直方向:y=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×\frac{qU}{md}•({\frac{l}{v})}^{2}=\frac{qU{l}^{2}}{2md{v}^{2}}$,
电子飞出电场时,水平分速度vx=v,竖直分速度:
vy=at=$\frac{qU}{md}•{\frac{l}{v}}^{\;}=\frac{qU{l}^{\;}}{md{v}^{\;}}$
则偏转角φ的正切值tanφ=$\frac{{v}_{y}}{{v}_{0}}=\frac{qU{l}^{\;}}{md{v}^{2}}$,
答:带电粒子射出电容器时在偏转电场中的偏转位移y为$\frac{qU{l}^{2}}{2md{v}^{2}}$,偏转角φ的正切值为$\frac{qU{l}^{\;}}{md{v}^{2}}$.
点评 本题考查了带电粒子在匀强电场中的偏转,其运动规律是类平抛运动,常用的方法是沿电场方向和垂直于电场的方向上进行正交分解,前者是初速度为零的匀加速直线运动,后者是匀速直线运动.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
17.一物体做匀变速直线运动,某时刻速度大小为2m/s,2s后的速度大小为8m/s,则该物体的加速度大小可能是( )
| A. | 3 m/s2 | B. | 4 m/s2 | C. | 5 m/s2 | D. | 8m/s2 |
18.以下列举的现象中,不考虑空气阻力,机械能不守恒的是( )
| A. | 雨点从高空自由下落 | B. | 足球运动员踢出的足球飞入球门 | ||
| C. | 小球沿光滑固定曲面下滑 | D. | 小球沿光滑固定斜面匀速向上运动 |
15.以下有关振动、波动和相对论内容的若干叙述中正确的是( )
| A. | 在“用单摆测定重力加速度”实验中,必须从最大位移处开始计时 | |
| B. | 光速不变原理是:真空中的光速在不同的惯性参考系中都是相同的 | |
| C. | 两列波相叠加产生干涉现象,振动加强区域与减弱区域应交替变化 | |
| D. | 光的偏振现象说明光波是横波 |
12. 如图所示,O、a、b三点是均匀介质中x轴上的三个质点,一列波长大于3m的简谐横波沿着x轴正方向传播,t=0时,波恰好传到质点a处,此时质点a开始向上运动,质点O处于最大位移处.t=1s时,质点a恰好第一次位于向上的最大位移处,下列说法中正确的是( )
如图所示,O、a、b三点是均匀介质中x轴上的三个质点,一列波长大于3m的简谐横波沿着x轴正方向传播,t=0时,波恰好传到质点a处,此时质点a开始向上运动,质点O处于最大位移处.t=1s时,质点a恰好第一次位于向上的最大位移处,下列说法中正确的是( )
 如图所示,O、a、b三点是均匀介质中x轴上的三个质点,一列波长大于3m的简谐横波沿着x轴正方向传播,t=0时,波恰好传到质点a处,此时质点a开始向上运动,质点O处于最大位移处.t=1s时,质点a恰好第一次位于向上的最大位移处,下列说法中正确的是( )
如图所示,O、a、b三点是均匀介质中x轴上的三个质点,一列波长大于3m的简谐横波沿着x轴正方向传播,t=0时,波恰好传到质点a处,此时质点a开始向上运动,质点O处于最大位移处.t=1s时,质点a恰好第一次位于向上的最大位移处,下列说法中正确的是( )| A. | 该波传播的波长一定为12m | |
| B. | 该波传播的周期一定为4s | |
| C. | 该波传播的波速一定为3m/s | |
| D. | t=6s时,质点b一定处于平衡位置且向上运动 | |
| E. | 波传到质点b以后两质点a、b 的位移始终大小相等、方向相反 |
19.关于《验证力的平行四边形定则》实验说法正确的是( )
| A. | 拉橡皮条时,橡皮条、细绳和弹簧测力计应贴近且平行于木板 | |
| B. | 两分力F1、F2的夹角应取90°,以方便计算合力的大小 | |
| C. | 两次拉橡皮条将橡皮条拉伸相同长度即可 | |
| D. | 实验中必须记录弹簧测力计的拉力的方向 |
16. 如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )
如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )
 如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )
如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )| A. | 磁铁对桌面的压力减小 | B. | 磁铁对桌面的压力不变 | ||
| C. | 磁铁受向左的摩擦力 | D. | 磁铁受向右的摩擦力 |
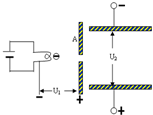 如图真空中炽热的金属丝发射的电子经过电压为U=1000V加速场后接着从A板的小孔处飞入电场强度E=5000N/C的竖直方向的偏转电场,设电子刚刚离开金属丝时速度为零.偏转电极长度L=6cm.求:电子离开偏转电场时的偏转位移y.
如图真空中炽热的金属丝发射的电子经过电压为U=1000V加速场后接着从A板的小孔处飞入电场强度E=5000N/C的竖直方向的偏转电场,设电子刚刚离开金属丝时速度为零.偏转电极长度L=6cm.求:电子离开偏转电场时的偏转位移y.