��Ŀ����
��1����ͼ1��ʾ��ABCΪһ�̶�����ֱƽ���ڵĹ⻬�����BC��ˮƽ��AB����BC��ƽ�����ӣ�����Ϊm1��С��Ӹ�λh���ɾ�ֹ��ʼ�ع���»����뾲ֹ�ڹ��BC��������Ϊm2��С������ײ����ײ��������˶�������ͬһˮƽ���ϣ�������ײ��������е����ʧ������ײ��С��m2���ٶȴ�Сv2��
��2����ײ�����е��������ݹ���������ѧ�����Ź㷺��Ӧ�ã�Ϊ��̽����һ���ɣ����Dz��ö���������ײ����ײǰ���ٶ���ͬһֱ���ϡ�����е����ʧ�ļ���ѧģ�ͣ���ͼ2��ʾ���ڹ̶��⻬ˮƽ����ϣ������ֱ�Ϊm1��m2��m3��mn-1��mn�������ɸ�����ֱ�߾�ֹ������У�����1�������Ek1���Ӷ���������������ײ���������е�n����������ײ���õĶ���Ek��Ek1֮��Ϊ��1����Ե�n����Ķ��ܴ���ϵ��k1n��
a����k1n��
b����m1=4m0��mk=m0��m0Ϊȷ������֪������m2Ϊ��ֵʱ��k1nֵ���

��2����ײ�����е��������ݹ���������ѧ�����Ź㷺��Ӧ�ã�Ϊ��̽����һ���ɣ����Dz��ö���������ײ����ײǰ���ٶ���ͬһֱ���ϡ�����е����ʧ�ļ���ѧģ�ͣ���ͼ2��ʾ���ڹ̶��⻬ˮƽ����ϣ������ֱ�Ϊm1��m2��m3��mn-1��mn�������ɸ�����ֱ�߾�ֹ������У�����1�������Ek1���Ӷ���������������ײ���������е�n����������ײ���õĶ���Ek��Ek1֮��Ϊ��1����Ե�n����Ķ��ܴ���ϵ��k1n��
a����k1n��
b����m1=4m0��mk=m0��m0Ϊȷ������֪������m2Ϊ��ֵʱ��k1nֵ���

��1������ײǰ���ٶ�Ϊ
�����ݻ�е���غ㶨�� m1gh=
m1
��
����ײ��m1��m2���ٶȷֱ�Ϊv1��v2�����ݶ����غ㶨�� m1v10=m1v1+m2v2 ��
������ײ��������е����ʧ
m1
=
m1
+
m2
��
�ڡ���ʽ�������v2=
��
���ٴ���â�v2=
��
��2��a���ɢ�ʽ�����ǵ� EK1=
m1V102
EK2=
m2V22 ��
���ݶ��ܴ���ϵ���Ķ��壬����1��2���� k12=
=
��
ͬ���ɵã���m2����m3��ײ���ܴ���ϵ��k13ӦΪ k13=
=
?
=
?
��
�������ƣ����Թ��ɵó������ܴ���ϵ��k1nӦΪ k1n=
=
?
��
=
?
��
��
�� k1n=
��
b����m1=4m0��m3=mo�����ʽ�ɵ� k13=64m02[
]2
Ϊʹk13���ֻ��ʹ
=
���m2+
ȡ��Сֵ��
��
��
=
����m2=2m0ʱ��k13�����
�𣺣�1����ײ��С��m2���ٶȴ�Сv2=
��
��2����m2=2m0 ʱ��k13ֵ���
| V | 210 |
| 1 |
| 2 |
| v | 210 |
����ײ��m1��m2���ٶȷֱ�Ϊv1��v2�����ݶ����غ㶨�� m1v10=m1v1+m2v2 ��
������ײ��������е����ʧ
| 1 |
| 2 |
| v | 210 |
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
�ڡ���ʽ�������v2=
| 2m1v10 |
| m1+m2 |
���ٴ���â�v2=
2m1
| ||
| m1+m2 |
��2��a���ɢ�ʽ�����ǵ� EK1=
| 1 |
| 2 |
EK2=
| 1 |
| 2 |
���ݶ��ܴ���ϵ���Ķ��壬����1��2���� k12=
| Ek2 |
| Ek1 |
| 4m1m2 |
| (m1+m2)2 |
ͬ���ɵã���m2����m3��ײ���ܴ���ϵ��k13ӦΪ k13=
| Ek3 |
| Ek1 |
| Ek2 |
| Ek1 |
| Ek3 |
| Ek2 |
| 4m1m2 |
| (m1+m2)2 |
| 4m2m3 |
| (m2+m3)2 |
�������ƣ����Թ��ɵó������ܴ���ϵ��k1nӦΪ k1n=
| Ekn |
| Ek1 |
| Ek2 |
| Ek1 |
| Ek3 |
| Ek2 |
| Ekn |
| Ek(n-1) |
| 4m1m2 |
| (m1+ m2)2 |
| 4m2m3 |
| (m2+ m3)2 |
| 4m(n-1)mn |
| (m(n-1)+ mn)2 |
�� k1n=
4n-1m1
| ||||||
| (m1+m2)2(m2+m3)2��(mn-1+mn)2 |
b����m1=4m0��m3=mo�����ʽ�ɵ� k13=64m02[
| m2 |
| (4m0+m2)(m0+m2) |
Ϊʹk13���ֻ��ʹ
| m2 |
| (4mo+m2)(m2+m0) |
| 1 | ||
4
|
4
| ||
| m2 |
��
|
| m2 |
| 2m0 | ||
|
�𣺣�1����ײ��С��m2���ٶȴ�Сv2=
2m1
| ||
| m1+m2 |
��2����m2=2m0 ʱ��k13ֵ���

��ϰ��ϵ�д�
�����Ŀ
 ��2008?������һģ����1����ͼ1��ʾ��������������Ϊ
��2008?������һģ����1����ͼ1��ʾ��������������Ϊ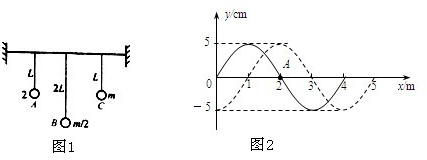

















 g
g
 ��
��





