题目内容
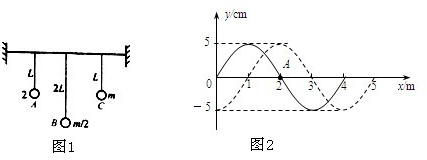
（1）如图1所示为受迫振动的演示装置，当单摆A振动起来后，通过水平悬绳迫使单摆B、C振动，则下列说法正确的是 ：
A．只有A、C摆振动周期相等
B．A摆的振幅比B摆小
C．C摆的振幅比B摆大
D． A、B、C三摆的振动周期相等
（2）在“用单摆测重力加速度”的实验中，若测得的重力加速度g值偏大，其原因可能是 ：
A．摆球质量太大
B．误将摆线长当成摆长，未加小球的半径
C．误将n次全振动记录为（n+1）次
D．单摆振幅偏小
（3）如图2所示，实线是一列简谐横波在t1=0时刻的波形图，虚线为t2=0.5s时的波形图，已知0＜t2-t1＜T，t1=0时，x=2m处的质点A正向y轴正方向振动．则：
①质点A的振动周期为 ；
②波的传播方向是 ；
③波速大小为 ；
④从t2时刻计时，x=1m处的质点的振动方程是 ．
A．只有A、C摆振动周期相等
B．A摆的振幅比B摆小
C．C摆的振幅比B摆大
D． A、B、C三摆的振动周期相等
（2）在“用单摆测重力加速度”的实验中，若测得的重力加速度g值偏大，其原因可能是
A．摆球质量太大
B．误将摆线长当成摆长，未加小球的半径
C．误将n次全振动记录为（n+1）次
D．单摆振幅偏小
（3）如图2所示，实线是一列简谐横波在t1=0时刻的波形图，虚线为t2=0.5s时的波形图，已知0＜t2-t1＜T，t1=0时，x=2m处的质点A正向y轴正方向振动．则：
①质点A的振动周期为
②波的传播方向是
③波速大小为
④从t2时刻计时，x=1m处的质点的振动方程是
分析：（1）由题意A做自由振动，B、C做受迫振动，受迫振动的周期等于驱动力的周期，即等于A的固有周期．C发生共振，振幅最大．
（2）根据单摆的周期公式得出g的表达式，再分析误差产生的原因．
（3）t1=0时，x=2m处的质点A正向y轴正方向振动，知波的传播方向．由根据波形的平移和0＜t2-t1＜T，确定出周期，求出波速的大小．根据t2时刻，x=1m处的质点的位移和速度大小，再写出其振动方程．
（2）根据单摆的周期公式得出g的表达式，再分析误差产生的原因．
（3）t1=0时，x=2m处的质点A正向y轴正方向振动，知波的传播方向．由根据波形的平移和0＜t2-t1＜T，确定出周期，求出波速的大小．根据t2时刻，x=1m处的质点的位移和速度大小，再写出其振动方程．
解答：解：（1）由题意，A做自由振动，其振动周期就等于其固有周期，而B、C在A产生的驱动力作用下做受迫振动，受迫振动的周期等于驱动力的周期，即等于A的固有周期，所以三个单摆的振动周期相等．由于C、A的摆长相等，则C的固有周期与驱动力周期相等，产生共振，其振幅振幅比B摆大．所以CD正确，AB错误．
故选CD
（2）由单摆周期公式T=2π
得，g=
．
A、由上式可知，g与摆球质量无关．故A错误．
B、若误将摆线长当成摆长，未加小球的半径，摆长l偏小，则g值偏小．故B错误．
C、单摆的周期T=
．若误将n次全振动记录为（n+1）次，T偏小，则g偏大．故C正确．
D、g与振幅无关．故D错误．
故选C
（3）①②t1=0时，x=2m处的质点A正向y轴正方向振动，则可知波的传播方向是沿x轴正方向．已知0＜t2-t1＜T，根据波形的平移得知，t2-t1=
，解得T=2s．③波速大小为v=
m/s=2m/s．④t2时刻，x=1m处的质点的位移为0，速度方向向下，振幅为A=5cm，则其振动方程为y=-Asin
t=-5sinπt（cm）．
故答案为：
（1）CD；（2）C；（3）①2s；②沿x轴正方向；③2m/s；④-5sinπt（cm）．
故选CD
（2）由单摆周期公式T=2π
|
| 4π2l |
| T2 |
A、由上式可知，g与摆球质量无关．故A错误．
B、若误将摆线长当成摆长，未加小球的半径，摆长l偏小，则g值偏小．故B错误．
C、单摆的周期T=
| t |
| n |
D、g与振幅无关．故D错误．
故选C
（3）①②t1=0时，x=2m处的质点A正向y轴正方向振动，则可知波的传播方向是沿x轴正方向．已知0＜t2-t1＜T，根据波形的平移得知，t2-t1=
| T |
| 4 |
| λ |
| T |
| 4 |
| 2 |
| 2π |
| T |
故答案为：
（1）CD；（2）C；（3）①2s；②沿x轴正方向；③2m/s；④-5sinπt（cm）．
点评：本题考查受迫振动的周期、共振现象、单摆的周期公式应用和波动图象的理解，难度选中．
练习册系列答案
相关题目
，其中r和R的意义见图7-1。
，其中r指考察点到球心的距离
，其中ρ为电荷体密度。这个式子的物理意义可以参照万有引力定律当中（条件部分）的“剥皮法则”理解〔
即为图7-2中虚线以内部分的总电量…〕。
，U内 = k
= 
，其中ε为绝对介电常数（真空中ε0 = 
，其它介质中ε= 
），εr则为相对介电常数，εr = 
。
= 
+
+
+ … +
q0U0 = 
C
= 
E2 
E2 。而且，这以结论适用于非匀强电场。
= ΔΩ = 
，ΔE2 = k
，即：ΔE1 = ΔE2 ，而它们的方向是相反的，故在P点激发的合场强为零。
，方向由P指向O点。
= Σ
= 0 ，最后的ΣE = ΣEz ，所以先求
，而且ΔScosθ为面元在xoy平面的投影，设为ΔS′
ΣΔS′
球面，每个
球面在x、y、z三个方向上分量均为
kπσ，能够对称抵消的将是y、z两个方向上的分量，因此ΣE = ΣEx …
= a ，如图7-7所示，试求空腔中各点的场强。
= r1 ，
= r2 ，则大球激发的场强为
= 
kρπr1 ，方向由O指向P
= 
kρπr2 ，方向由P指向O′
kρπa ，方向均沿O → O′，空腔里的电场是匀强电场。
πkρq〔
?
〕。
= r ，以无穷远为参考点，试求P点的电势UP 。
段，各段在P点形成的电势相同，而且它们是标量叠加。
；结论不会改变。
= k
·
= kσΔΩ
；（2）球心电势仍为k
，但其它各点的电势将随电量的分布情况的不同而不同（内部不再是等势体，球面不再是等势面）。
－ k
+ k
。
+ k
+ k
= 0
q
+ k
q ；（2）UB = k
(1－
) 。
UA ；UB′= 
UA + 
UB 。
U′
（U1 + U2 + U3 + U4）。
+ U半球面
－ UP 。
是以B为圆心、L为半径的半圆。A处放有电量为q的电荷，B处放有电量为－q的点电荷。试问：（1）将单位正电荷从O点沿
移到D点，电场力对它做了多少功？（2）将单位负电荷从D点沿AB的延长线移到无穷远处去，电场力对它做多少功？
+ k
= 0
+ k
= －
；（2）
。 
；（2）Ek1 = 
k
，Ek2 = 
k
；（3）k
。
+
+
）。
= 2 k
+ k
+ 
mv2 + 
2m
。
〕。
、A板内侧电量
，B板内侧电量?
、B板外侧电量
；（2）A板外侧空间场强2πk
，方向垂直A板向外，A、B板之间空间场强2πk
，方向由A垂直指向B，B板外侧空间场强2πk
，方向垂直B板向外；（3）A、B两板的电势差为2πkd
，A板电势高。
）？如果在板间充满相对介电常数为εr的电介质，是否会影响四个面的电荷分布（答：不会）？是否会影响三个空间的场强（答：只会影响Ⅱ空间的场强）？
·
（方向相左），内侧受力
·
（方向向右），它们合成即可，结论为F = 
Q1Q2 ，排斥力。〕
= 
，即 
= 
关系求解，比较常规（上下部分的场强相等）。
? 
）
Q ，介质部分的电量为
Q ；（2）整个空间的场强均为
；（3）
Q 。
Q 。
+ 
= 
解C′即可。
+ 
= 
C ；（2）
C 。
+
+
= 0
+ 
= 
，Q2′= 
，这样系统的储能就可以用
得出了。
；（2）
。
+ 
= 
。
为“和矢量”。
，其中α为
和
的夹角。
在
、
之间，和
夹角β= arcsin
= 
－
。
为“被减数矢量”，
为“减数矢量”，
为“差矢量”。
，其中θ为
和
的夹角。
T内和在
T内的平均加速度大小。
T的过程，A到C点对应
T的过程。这三点的速度矢量分别设为
、
和
。
= 
得：
= 
，
= 
= 
－
，
= 
－
，根据三角形法则，它们在图3中的大小、方向已绘出（
的“三角形”已被拉伸成一条直线）。
= 
= 
= 
，且：
= 
= 
，
= 2
= 
= 
= 
= 
，
= 
= 
= 
。
×
= 
称“矢量的叉积”，它是一个新的矢量。
和
的夹角。意义：
的大小对应由
和
作成的平行四边形的面积。
和
确定的平面，并由右手螺旋定则确定方向，如图4所示。
×
≠
×
，但有：
×
= －
×
·
= c
和
的夹角。
= 0 ，或 
= 0 ，
= 0
= 0 ，或ΣM+ =ΣM- 
= 
，即：N2 = 
，β在0到180°之间取值，N2的极值讨论是很容易的。
⑴
- R） ⑵
= 2Rcosθ ⑶
。
R 。
。
= 
①
= 
②
。
。
= F′。
。
解F的大小，由tgα= 
解F的方向（设α为F和斜面的夹角）。
，方向和斜面夹角α= arctg(
)指向斜面内部。
= 
= 
⑵