题目内容
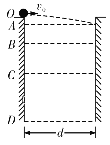
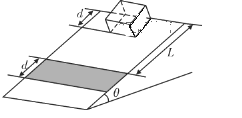
【题目】如图所示,倾角为37°的光滑斜面上粘贴有一厚度不计、宽度为d=0.2 m的橡胶带,橡胶带的上表面与斜面位于同一平面内,其上、下边缘与斜面的上、下边缘平行,橡胶带的上边缘到斜面的顶端距离为L=0.4 m,现将质量为m=1 kg、质量分布均匀、宽度为d的薄矩形板上边缘与斜面顶端平齐且从斜面顶端静止释放.已知矩形板与橡胶带之间的动摩擦因数为0.5,重力加速度取g=10 m/s2,sin 37°=0.6,cos 37°=0.8,不计空气阻力,矩形板由斜面顶端静止释放下滑到完全离开橡胶带的过程中(此过程矩形板始终在斜面上),下列说法正确的是
A.矩形板受到的摩擦力恒为Ff=4 N
B.矩形板的重力做功为WG=2.4 J
C.产生的热量为Q=0.8 J
D.矩形板的上边缘穿过橡胶带下边缘时速度大小为![]() m/s
m/s
【答案】CD
【解析】
A.矩形板在滑过橡胶带的过程中对橡胶带的正压力是变化的,所以矩形板受摩擦力是变化的,故A错误;
B.重力做功WG=mg(L+d)sin θ=3.6 J,所以B错误;
C.产生的热量等于克服摩擦力做功Q=2×![]() μmgcos θ·d=0.8 J,所以C正确;
μmgcos θ·d=0.8 J,所以C正确;
D.根据动能定理:WG-Q=![]() mv2-0,解得v=
mv2-0,解得v=![]() m/s,所以D正确.
m/s,所以D正确.

练习册系列答案
相关题目