题目内容
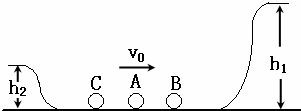 如图所示,A、B、C三个小球位于同一水平面上,他们大小相同,B、C质量相等,都是A球质量的一半,B、C两球开始静止,A球以速度v0向右运动,要使A球能分别将B、C两球撞上高度分别为h1=0.8m、h2=0.2m的平台(且都不再返回).已知A和B的碰撞没有机械能损失,A和C碰后粘在一起,不计一切摩擦,求v0的范围.
如图所示,A、B、C三个小球位于同一水平面上,他们大小相同,B、C质量相等,都是A球质量的一半,B、C两球开始静止,A球以速度v0向右运动,要使A球能分别将B、C两球撞上高度分别为h1=0.8m、h2=0.2m的平台(且都不再返回).已知A和B的碰撞没有机械能损失,A和C碰后粘在一起,不计一切摩擦,求v0的范围.分析:小球碰撞过程中动滑轮守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出速度大小的范围.
解答:解:设B、C质量为m,A质量为2m,A、B碰后瞬间速度为v1、v2,
由动量守恒定律可得:2mv0=2mv1+mv2,
由能量守恒定律可得:
2mv02=
2mv12+
mv22,
解出:v1=
,v2=
,
欲使B能达到h1高度,
mv22≥mgh1,解得:v0≥3m/s,
欲使A与B碰后不能达到h1高度,
2mv12≤2mgh2,解得v0≤12m/s,
欲使A与C碰后能一起上升到h2高度,
由动量守恒定律得:2mv1=3mv2,
由能量守恒定律得:
3mv32≥3mgh,得出v0≥9m/s,
综上所述可知:9m/s≤v0≤12m/s;
答:v0的范围是9m/s≤v0≤12m/s.
由动量守恒定律可得:2mv0=2mv1+mv2,
由能量守恒定律可得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解出:v1=
| v0 |
| 3 |
| 4v0 |
| 3 |
欲使B能达到h1高度,
| 1 |
| 2 |
欲使A与B碰后不能达到h1高度,
| 1 |
| 2 |
欲使A与C碰后能一起上升到h2高度,
由动量守恒定律得:2mv1=3mv2,
由能量守恒定律得:
| 1 |
| 2 |
综上所述可知:9m/s≤v0≤12m/s;
答:v0的范围是9m/s≤v0≤12m/s.
点评:分析清楚物体运动过程确定需要满足的条件、应用动量守恒定律、能量守恒定律即可正确解题.

练习册系列答案
相关题目

 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )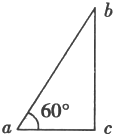 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,