题目内容
【题目】如图所示,竖直平面内有固定的弯折形滑杆轨道ACB和ADB,AC平行于DB,AD平行于CB.一小圆环(图中未画出)先后套在ACB、ADB上,从A点由静止释放,滑到B点所用的时间为t1、t2,到达B点的速度大小为v1、v2.已知小圆环与两条轨道之间的动摩擦因数都相同,不计弯折处能量损失.下列关系式成立的是( )
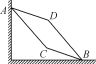
A. t1>t2 B. t1<t2 C. v1>v2 D. v1<v2
【答案】B
【解析】
通过作v-t图象分析时间关系,根据动能定理分析小滑块沿ACB和ADB下滑到B点速度大小关系;
A、根据牛顿第二定律知:AC段与DB段加速度相同,AD段与CB段加速度相同,且AC段与DB段加速度较大,作出两个过程的![]() 图象如图所示:
图象如图所示:
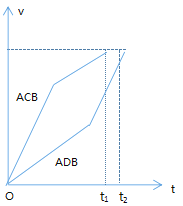
结合![]() 图象与时间轴所围的面积表示位移,两个过程位移相等,则有
图象与时间轴所围的面积表示位移,两个过程位移相等,则有![]() ,故选项A错误,B正确;
,故选项A错误,B正确;
C、设任一斜面的倾角为![]() ,斜面长为L,则小圆环的摩擦力为:
,斜面长为L,则小圆环的摩擦力为:![]()
则小圆环沿斜面下滑时摩擦力的功为:![]()
其中![]() 为斜面的水平底边的长度;
为斜面的水平底边的长度;
根据上面分析可知:小圆环沿ACB或ADB下滑时摩擦力的功和重力的功相同,根据动能定理可知到达B点时动能相等,即![]() ,故选项CD错误。
,故选项CD错误。

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目