题目内容
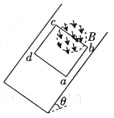
【题目】如图所示,粗糙斜面的倾角=37°,半径r=0.5m的圆形区域内存在着垂直于斜面向下的匀强磁场,一个刚性、单匝正方形线框bcd的bc边恰好与圆形磁场的直径重合.已知线框质量m=0.2kg,电阻R=0.25Ω,边长L=1.2m,与斜面间的动摩擦因数=0.5。从t=0时起,磁场的磁感应强度按B=2—![]() (T)的规律变化,开始时线框静止在斜面上,设最大静摩擦力等于滑动摩擦力,g取10m/s2,sin37°=0.6,cos37°=0.8,则
(T)的规律变化,开始时线框静止在斜面上,设最大静摩擦力等于滑动摩擦力,g取10m/s2,sin37°=0.6,cos37°=0.8,则
A. 正方形线框运动前回路中电流大小为1A
B. 线框刚要运动时,磁场的磁感应强度大小为0.6T
C. 线框在斜面上可保持静止的时间为0.8πs
D. 线框刚要运动时bc边受到的安培力大小为0.48N
【答案】AC
【解析】A.由法拉第电磁感应定律有:
正方形线框中产生的感应电动势E=n△Φ/△t=![]()
由题意可知n=1,△B/△t=2/π(T/s)
解得:E=0.25V
由闭合电路欧姆定律有:E=IR
解得:I=1A,故A正确;
B.对线框bc边处于磁场的部分受力分析如图所示,

设当线框恰好沿斜面向下运动时,磁场的磁感应强度为B;
安培力F=BI2r
由力的平衡条件有:
mgsinθ=F+f=2BIr+μmgcosθ
解得:F=0.4N,B=0.4T,故B错误,D错误;
C.由B=2—![]() t可得:
t可得:
线框在斜面上可保持静止的时间为
t=0.8πs.故C正确;
故选:AC。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目