��Ŀ����
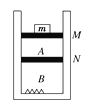
����Ŀ����ͼ��ʾ������m��0.2kg���㹻����U���ν�������abcd�������������37���Ĺ⻬��Եб���ϣ�����bc�γ�L��1m������R��0.5����������費�ơ���һ�����͵����뵼�����ͬ�ĵ����PQ��ֱ�����ڵ����ϣ����뵼��Ӵ����ã����뵼��䶯Ħ����������0.5�������²��������̶���б��Ĺ⻬��Ե��������efΪ�磬�²���ǿ�ų�������б�����ϣ��Ÿ�Ӧǿ�ȴ�СΪB��1T���ϲ�ų�B������ֱб�����ϡ���ʼbcfe�����������Σ�������ϸ�߿�����붨���ֽ�bc���е���������ΪM������������ϸ����ֱʱ�뵼��bc�δ�ֱ���ֽ������ɾ�ֹ�ͷš������Ħ�������ڻ���Ħ������sin37����0.6��gȡ10m/s2��

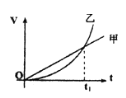
(1)��M��0.3kg����B����B��1T�����˶���õ�����ٶ�
(2)��M��0.3kg����B����B��1T���ڵ��쿪ʼ�˶����������ٶȵĹ����У���PQ�����Ľ�����Q��0.15J��ͨ������ĵ����q��1.5C����˹�������Ħ�����ӵ�������E��
(3)��M��0.1kg����B���仯����ΪBt��kt��k��2T/s�����ʱ��������쿪ʼ������
���𰸡�(1)![]() ��(2)
��(2)![]() ��2.3J��(3)t��0.4s
��2.3J��(3)t��0.4s
��������
(1) ������ٶ����ʱ���У�![]()
![]()
�������ݽ�ã�![]() ��
��
(2) ����Ӹտ�ʼ�˶����ٶ����Ĺ����У��������غ㶨�ɵã�
![]()
��![]() ������
������![]()
ƽ����Ӧ�綯��Ϊ��![]()
������ã�![]()
(3) ���ݷ����ڵ�Ÿ�Ӧ���ɣ���·�еĵ綯�ƣ�![]()
��Ӧ������![]()
����ʱ��t���Ÿ�Ӧǿ�ȣ�![]()
���������ܵ��İ�������![]()
Ħ������![]()
��![]() ʱ����������ո�Ҫ�����ƶ���������ã�
ʱ����������ո�Ҫ�����ƶ���������ã�![]() ��
��

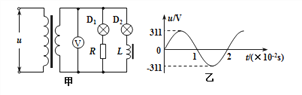
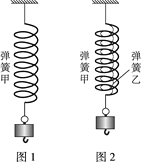
����Ŀ����̽�������͵����쳤�Ĺ�ϵʱ��ijͬѧ�Ȱ�ͼ1�Ե��ɼ���̽����Ȼ���ԭ����ͬ�ĵ��ɼ͵����Ҳ���������ͼ2����̽��.�ڵ������ڣ�������Ϊm=50g�Ĺ���������ڵ����¶ˣ��ֱ���ͼ1��ͼ2�е��ɵij���L1��L2���±���ʾ.
������� | 1 | 2 | 3 | 4 |
L1/cm | 36.05 | 38.04 | 40.02 | 42.01 |
L2/cm | 29.32 | 29.65 | 29.97 | 30.30 |
��֪�������ٶ�g=9.8m/s2��Ҫ���ܶ�����ò������ݣ����㵯�ɼľ���ϵ��k1=______N/m�����������λ��Ч���֣�.�ɱ������ݼ���������ҵľ���ϵ��k2=______N/m�����������λ��Ч���֣�.