��Ŀ����
����Ŀ����ͼ��ʾ�������=37�����㹻��б����̶���ˮƽ���ϣ������ͬ��ľ��B��C������б���ϣ�B��C�ij��ȷֱ�ΪL��0.5L�������ֱ�Ϊm��0.5m������֮��ľ���ΪL����б��֮��Ķ�Ħ��������2=0��5��������Ϊ0��25m�����A������Ϊ�ʵ㣩�����B�Ķ��ˣ�ͬʱ�����B��������A��B���Ӿ�ֹ��ʼ�ȼ���ֱ���˶�����B��C��ײǰ��һ˲�䣬�����C����������ʱAǡ�û���B����B��C��ײ��ճ��һ����ײʱ�伫�̣����������ٶ�ȡg��sin37��=0.6����
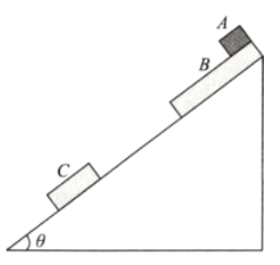
��1�����A��ľ��B֮��Ķ�Ħ��������1��
��2���ӿ�ʼ�˶���B��C��ײ��ϵͳ��Ħ������������Q��
��3����B��C��ײ��B��C�����A��ǡ�������˶�����A��C�ϻ��е�ʱ�䡣
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
��1�� A��B�ϻ��У���������ͼ��a��
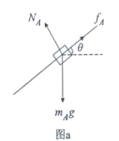
��ţ�ٵ�һ����
mAgsin![]() -��1mAgcos
-��1mAgcos![]() = mAaA
= mAaA
��
aA=��0.6-0.8��1��g
B������ͼ��b����
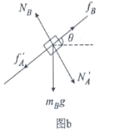
��ţ�ٵڶ�����
mBgsin![]() +��1mAgcos
+��1mAgcos![]() -��2��mA+mB��gcos
-��2��mA+mB��gcos![]() = mBaB
= mBaB
��
aB=��0.1-0.2��1��g
���˶�ѧ����
2L=![]()
L=![]()
�������
��1=![]()
��2��A��B�ϻ��У�����������
Q1=��1mAgcos![]() ��L
��L
B��б���ϻ��У�����������
Q2=��2��mA+mB��gcos![]() ��L
��L
���ԣ�ϵͳ��Ħ������������
Q=Q1+Q2=![]()
��3��B��C��ײǰ��A���ٶ�Ϊ
vA=![]()
B���ٶ�Ϊ
vB=![]()
B��C��ײ��ϵͳ�����غ�
mBvB=��mC+mB��v��
B��C�����A�����˶���A��C�ϻ��е�ʱ��Ϊ��
t=![]()

 �Ķ��쳵ϵ�д�
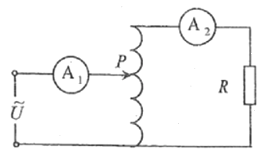
�Ķ��쳵ϵ�д�����Ŀ��ijͬѧ������̽��С���ٶ���ʱ��仯�Ĺ�����ʵ��ʱ��
(1)����ʱ������_______��ѡ�����ֱ������Դ��ʵ�������_______�����ɴ����һ��ֽ����
A��Ӧ�Ƚ�ͨ��Դ���ڴ���ʱ����ʼ�������ͷų�
B��Ӧ���ͷ�С�����ٽ�ͨ��Դ��ʼ���
C���ͷ�С����ͬʱͨ��Դ��ʼ���
D�����ͷ�С�����Ƚ�ͨ��Դ����ʱ����ʼ��㶼����
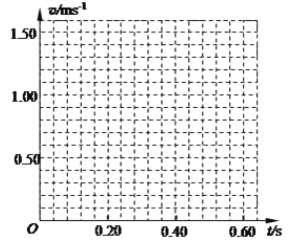
(2)��֪��ʱ������ʱ����Ϊ0.02s����ͬѧ������Ⱥ�˳��ÿ��4����ȡ1�������㣬�õ���O��A��B��C��D�ȼ��������㣬��ͼ��ʾ������������������֮���ʱ����Ϊ________s���ÿ̶ȳ�����OA��1.50cm��AB��1.90cm��BC��2.30cm��CD��2.70cm����C��ʱֽ�����ٶȴ�СΪ________m/s��
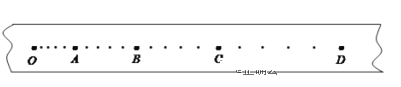
(3)��ͬѧ����ij��ֽ��ͨ�����㣬�õ��˸���������ٶȣ��������±������ݱ������ݣ�������������ϵ������v��tͼ����1��������Ϊ��ʱ��㣩
������ | 1 | 2 | 3 | 4 | 5 | 6 |
����������ٶ�m/s | 0.50 | 0.71 | 0.89 | 1.10 | 1.30 | 1.51 |
��___________��