题目内容
 如图所示,匀强电场方向沿x轴的正方向,场强为E.在A(l,0)点有一个质量为m,电荷量为q 的粒子,以沿 y 轴负方向的初速度v0开始运动,经过一段时间到达B(0,-l)点,(不计重力作用).求:
如图所示,匀强电场方向沿x轴的正方向,场强为E.在A(l,0)点有一个质量为m,电荷量为q 的粒子,以沿 y 轴负方向的初速度v0开始运动,经过一段时间到达B(0,-l)点,(不计重力作用).求:(1)粒子的初速度v0的大小.
(2)当粒子到达B点时,电场力对粒子做功的瞬时功率.
分析:(1)粒子在y方向不受力,做匀速直线运动;在x方向由于受恒定的电场力,做匀加速直线运动.所以粒子做的是类平抛运动.由题可知水平位移和竖直位移均为l,由牛顿第二定律求出加速度,分别运用运动学公式研究水平方向和竖直求解.
(2)电场力的瞬时功率等于电场力乘以电场力方向的速度vx,由vx=at和功率公式求解.
(2)电场力的瞬时功率等于电场力乘以电场力方向的速度vx,由vx=at和功率公式求解.
解答:解:(1)设粒子的初速度为v0,则:
在y方向上有:y=v0t
在x方向上有:x=
at2=
t2=
(
)2
又x=y=l
可得:v0=
(2)设粒子到达B点时的速度为v,
则电场力做功的瞬时功率为:P=qEvx
由运动学公式可得:vx=
=
故P=qEvx=qE
答:(1)粒子的初速度v0的大小为
.
(2)当粒子到达B点时,电场力对粒子做功的瞬时功率为qE
.
在y方向上有:y=v0t
在x方向上有:x=
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
| 1 |
| 2 |
| qE |
| m |
| l |
| v0 |
又x=y=l
可得:v0=
|
(2)设粒子到达B点时的速度为v,
则电场力做功的瞬时功率为:P=qEvx
由运动学公式可得:vx=
| 2al |
|
故P=qEvx=qE
|
答:(1)粒子的初速度v0的大小为
|
(2)当粒子到达B点时,电场力对粒子做功的瞬时功率为qE
|
点评:本题是电场中基本的题型,考查分析和解决问题的能力.对于功率,不能用P=qEv=
,应采运用分解方法,得到P=qEvy.
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
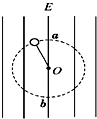 如图所示,在竖直方上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )
如图所示,在竖直方上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )| A、小球一定带正电 | B、电场力跟重力平衡 | C、小球在从a点运动到b点的过程中,电势能一定增大 | D、小球在运动过程中机械能守恒 |
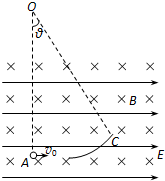 在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg、电荷量q=+9.0×10-4 C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求:
在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg、电荷量q=+9.0×10-4 C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求:



 (3)粒子在电、磁场中运动的总时间。
(3)粒子在电、磁场中运动的总时间。