题目内容
11.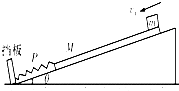 如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1.0kg的木板与轻弹簧接触但不拴接,弹簧与斜面平行且为原长,在木板右上端放一质量为m=2.0kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面粗糙部分间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3m/s、方向平行斜面向下的速度,沿木板向下运动.当弹簧被压缩x=0.5m到P点时,金属块与木板刚好达到相对静止,且此后运动过程中,两者一直没有发生相对运动.设金属块从开始运动到与木块达到相同速度共用时间t=0.75s,之后木板压缩弹簧至最短,然后木板向上运动,弹簧弹开木板,弹簧始终处于弹性限度内,已知sinθ=0.28、cosθ=0.96(g取10m/s2)(结果保留两位有效数字),求:
如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1.0kg的木板与轻弹簧接触但不拴接,弹簧与斜面平行且为原长,在木板右上端放一质量为m=2.0kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面粗糙部分间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3m/s、方向平行斜面向下的速度,沿木板向下运动.当弹簧被压缩x=0.5m到P点时,金属块与木板刚好达到相对静止,且此后运动过程中,两者一直没有发生相对运动.设金属块从开始运动到与木块达到相同速度共用时间t=0.75s,之后木板压缩弹簧至最短,然后木板向上运动,弹簧弹开木板,弹簧始终处于弹性限度内,已知sinθ=0.28、cosθ=0.96(g取10m/s2)(结果保留两位有效数字),求:(1)求木板开始运动瞬间木板和小金属块的加速度;
(2)求弹簧被压缩到P点时的弹性势能是多少?
(3)假设木板在由P点压缩弹簧到弹回到P点过程中不受斜面摩擦力作用,木板离开弹簧后沿斜面向上滑行的距离?
分析 (1)运用隔离法分别对金属块和长木板进行受力分析,根据牛顿第二定律求加速度;
(2)根据动能定理求得弹簧压缩过程中做的功,再根据弹力做功与弹性势能变化的关系求得弹簧的弹性势能;
(3)根据能量转化和守恒定律求得木板离开弹簧后的速度,再根据动能定理求得木板上滑的最大距离.
解答 解:(1)对金属块,由牛顿第二定律可知:μ1mgcosθ-mgsin θ=ma
解得:a=4.4 m/s2,沿斜面向上
木板受到金属块的滑动摩擦力F1=μ1mgcosθ=14.4 N,沿斜面向下
木板受到斜面的滑动摩擦力F2=μ2(M+m)gcosθ=7.2 N,沿斜面向上
木板开始运动瞬间的加速度a0=$\frac{Mgsinθ+{F}_{1}-{F}_{2}}{M}$=10 m/s2,沿斜面向下
(2)设金属块和木板达到共同速度为v2,对金属块,应用速度公式有
v2=v1-at=2.0 m/s
在此过程中分析木板,设弹簧对木板做功为W,其余力做功为Ma0x,
对木板运用动能定理得:Ma0x+W=$\frac{1}{2}$Mv22
解得W=-3.0 J,
说明此时弹簧的弹性势能Ep=3.0 J
(3)从金属块和木板达到共速后压缩弹簧到速度减小为0后反向弹回刚离开弹簧的整个过程,设弹簧恢复原长时木板和金属块的速度为v3,在此过程中对木板和金属块整体来说,由能量的转化和守恒得:
Ep-(F2+Mgsinθ+mgsinθ)x=$\frac{1}{2}$(M+m)v32-$\frac{1}{2}$(M+m)v22
木板离开弹簧后,设滑行距离为s,对整体由动能定理得:
-(M+m)g(μ2cos θ+sin θ)s=0-$\frac{1}{2}$(M+m)v32
解得:s=0.077 m
答:(1)木板开始运动瞬间木板的加速度大小为10 m/s2,方向沿斜面向下,小金属块的加速度大小为4.4 m/s2,方向沿斜面向上;
(2)弹簧被压缩到P点时的弹性势能是3.0 J;
(3)假设木板在由P点压缩弹簧到弹回到P点过程中不受斜面摩擦力作用,木板离开弹簧后沿斜面向上滑行的距离为0.077m.
点评 在应用牛顿运动定律和运动学公式解决问题时,要注意运动过程的分析,此类问题,还要对整个运动进行分段处理.

 在空军演练中,某空降兵从悬停的直升机上跳下,他从跳离飞机到落地的过程中沿竖直方向运动的v-t图象如图所示,则下列说法中正确的是( )
在空军演练中,某空降兵从悬停的直升机上跳下,他从跳离飞机到落地的过程中沿竖直方向运动的v-t图象如图所示,则下列说法中正确的是( )| A. | 0-t1内空降兵和伞整体所受重力大于空气阻力,t1-t2内整体所受重力小于空气阻力 | |
| B. | 0-t1内做加速度逐渐减小的加速运动,t1-t2内做加速度减小的减速运动 | |
| C. | t1时刻打开降落伞,以后做匀减速运动至t2时刻 | |
| D. | 从速度时间图象上可以看出,在降落伞打开前后空降兵和伞整体所受空气阻力都随着速度的增大而增大 |
 如图所示是示波器原理图.电子经电压为U1的电场加速后,射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,离荧光屏中心O的侧移为y.单位偏转电压引起的偏转距离($\frac{y}{{U}_{2}}$)称为示波器的灵敏度.下列哪些方法可以提高示波器的灵敏度( )
如图所示是示波器原理图.电子经电压为U1的电场加速后,射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,离荧光屏中心O的侧移为y.单位偏转电压引起的偏转距离($\frac{y}{{U}_{2}}$)称为示波器的灵敏度.下列哪些方法可以提高示波器的灵敏度( )| A. | 升高加速电压U1 | B. | 降低偏转电场电压U2 | ||
| C. | 增大极板的长度 | D. | 增大极板间的距离 |
| A. | 物体在某一时刻的瞬时速度就是瞬时速率 | |
| B. | 运动物体在某段时间内位移为零,则其运动速率也一定为零 | |
| C. | 速度变化得越多,加速度就越大 | |
| D. | 速度变化得越快,加速度就越大 |

| A. | M点场强小于N点场强 | |
| B. | M点电势低于N点电势 | |
| C. | 正电荷在M点受到的电场力方向由M指向N | |
| D. | 若E为M点的场强,则M、N两点间电势差等于E•d |
 目前智能手机普遍采用了电容屏.电容触摸屏是利用人体的电流感应进行工作的.当手指触摸电容触摸屏时,手指和屏的夹层工作面形成一个电容器,因为工作面上接有高频信号,电流通过电容器分别从屏的四个角上的电极中流出,并且流经这四个电极的电流与手指到四角的距离成正比,控制器通过对这四个电流比例的精确计算,得出触摸点的位置.对于触摸屏,下列说法正确的是( )
目前智能手机普遍采用了电容屏.电容触摸屏是利用人体的电流感应进行工作的.当手指触摸电容触摸屏时,手指和屏的夹层工作面形成一个电容器,因为工作面上接有高频信号,电流通过电容器分别从屏的四个角上的电极中流出,并且流经这四个电极的电流与手指到四角的距离成正比,控制器通过对这四个电流比例的精确计算,得出触摸点的位置.对于触摸屏,下列说法正确的是( )| A. | 使用绝缘笔,在电容屏上也能进行触控操作 | |
| B. | 手指与屏的接触面积变大时,电容变小 | |
| C. | 电容触摸屏只需要触摸,不需要压力即能产生位置信号 | |
| D. | 手指压力变大时,由于手指与屏的夹层工作面距离变小,电容变大 |
 如图所示,在倾角为37°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是75m,g取10m/s2.求:
如图所示,在倾角为37°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是75m,g取10m/s2.求: 如图所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
如图所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.