题目内容
6. 如图所示,在倾角为37°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是75m,g取10m/s2.求:
如图所示,在倾角为37°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是75m,g取10m/s2.求:(1)物体在空中运动的时间;
(2)物体抛出时速度的大小;
(3)物体抛出后多长时间距离斜面最远?
分析 (1)根据平抛运动的竖直位移,结合位移时间公式求出平抛运动的时间.
(2)根据水平位移和时间,求出物体抛出的速度大小.
(3)当物体的速度方向与斜面平行时,距离斜面最远,结合速度时间公式求出距离斜面最远的时间.
解答 解:(1)根据$ssin37°=\frac{1}{2}g{t}^{2}$得物体在空中运动的时间为:
t=$\sqrt{\frac{2ssin37°}{g}}=\sqrt{\frac{2×75×0.6}{10}}s=3s$.
(2)物体抛出的速度为:${v}_{0}=\frac{scos37°}{t}=\frac{75×0.8}{3}m/s=20m/s$.
(3)当物体的速度与斜面平行时,距离斜面最远,根据$tan37°=\frac{{v}_{y}}{{v}_{0}}=\frac{gt′}{{v}_{0}}$得:
$t′=\frac{{v}_{0}tan37°}{g}=\frac{20×\frac{3}{4}}{10}s=1.5s$.
答:(1)物体在空中运动的时间为3s;
(2)物体抛出时速度的大小为20m/s;
(3)物体抛出后1.5s时间距离斜面最远.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
相关题目
16.2013年1月15日上午10时许,陕西省蒲城县某花炮厂发生爆炸,爆炸没有造成人员伤亡,初步断定是因空气干燥,炸药堆放时间过长,由静电引发了爆炸.摩擦可以产生静电,原来甲、乙、丙三物体都不带电,今使甲、乙两物体相互摩擦后,乙物体再与丙物体接触,最后,得知甲物体带正电1.6×10-15 C,丙物体带电8×10-16 C.则对于最后乙、丙两物体的带电情况,下列说法中正确的是( )
| A. | 乙物体一定带有负电荷8×10-16C | B. | 乙物体可能带有负电荷2.4×10-15C | ||
| C. | 丙物体一定带有正电荷8×10-16C | D. | 丙物体一定带有负电荷2.4×10-15C |
17.一物体做匀变速直线运动,某时刻速度大小为2m/s,2s后的速度大小为8m/s,则该物体的加速度大小可能是( )
| A. | 3 m/s2 | B. | 4 m/s2 | C. | 5 m/s2 | D. | 8m/s2 |
14.某学校学生在开展“测金属电阻率”研究性学习括动中,对有关金属(灯泡中的钨丝)、半导体(二极管)、合金(标准电阻),及超导材料的电阻率查阅了大量资料,提出了下列一些说法,你认为正确的有 ( )
| A. | 金属温度计是利用金属材料的电阻率随温度升高而不发生显著变化制成的 | |
| B. | 标准电阻是利用合金材料的电阻率几乎不随温度变化而变化制成的 | |
| C. | 半导体材料的电阻率随温度升高而增大 | |
| D. | 当温度接近绝对零度时,某种材料电阻率突然为零,这种现象叫超导现象 |
18.以下列举的现象中,不考虑空气阻力,机械能不守恒的是( )
| A. | 雨点从高空自由下落 | B. | 足球运动员踢出的足球飞入球门 | ||
| C. | 小球沿光滑固定曲面下滑 | D. | 小球沿光滑固定斜面匀速向上运动 |
15.以下有关振动、波动和相对论内容的若干叙述中正确的是( )
| A. | 在“用单摆测定重力加速度”实验中,必须从最大位移处开始计时 | |
| B. | 光速不变原理是:真空中的光速在不同的惯性参考系中都是相同的 | |
| C. | 两列波相叠加产生干涉现象,振动加强区域与减弱区域应交替变化 | |
| D. | 光的偏振现象说明光波是横波 |
16. 如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )
如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )
 如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )
如图所示,条形磁铁放在水平桌面上,其正上方略偏右处固定一根直导线,导线和磁铁垂直,并通以垂直纸面向外的电流,则( )| A. | 磁铁对桌面的压力减小 | B. | 磁铁对桌面的压力不变 | ||
| C. | 磁铁受向左的摩擦力 | D. | 磁铁受向右的摩擦力 |

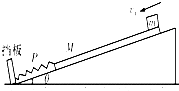 如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1.0kg的木板与轻弹簧接触但不拴接,弹簧与斜面平行且为原长,在木板右上端放一质量为m=2.0kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面粗糙部分间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3m/s、方向平行斜面向下的速度,沿木板向下运动.当弹簧被压缩x=0.5m到P点时,金属块与木板刚好达到相对静止,且此后运动过程中,两者一直没有发生相对运动.设金属块从开始运动到与木块达到相同速度共用时间t=0.75s,之后木板压缩弹簧至最短,然后木板向上运动,弹簧弹开木板,弹簧始终处于弹性限度内,已知sinθ=0.28、cosθ=0.96(g取10m/s2)(结果保留两位有效数字),求:
如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1.0kg的木板与轻弹簧接触但不拴接,弹簧与斜面平行且为原长,在木板右上端放一质量为m=2.0kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面粗糙部分间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3m/s、方向平行斜面向下的速度,沿木板向下运动.当弹簧被压缩x=0.5m到P点时,金属块与木板刚好达到相对静止,且此后运动过程中,两者一直没有发生相对运动.设金属块从开始运动到与木块达到相同速度共用时间t=0.75s,之后木板压缩弹簧至最短,然后木板向上运动,弹簧弹开木板,弹簧始终处于弹性限度内,已知sinθ=0.28、cosθ=0.96(g取10m/s2)(结果保留两位有效数字),求: