题目内容
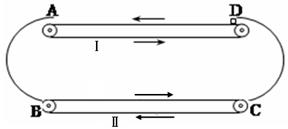
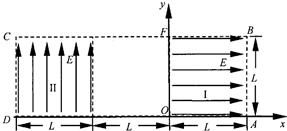
(18分)如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑轨道固定于竖直平面内,A、D之间放一水平传送带Ⅰ,B、C之间放一水平传送带Ⅱ,传送带Ⅰ以V1=6m/s的速度沿图示方向匀速运动,传送带Ⅱ以V2=8m/s的速度沿图示方向匀速运动。现将质量为m=4kg的物块从传送带Ⅰ的右端由静止放上传送带,物块运动第一次到A时恰好能沿半圆轨道滑下。物块与传送带Ⅱ间的动摩擦因数为μ2=0.125,不计物块的大小及传送带与半圆轨道间的间隙,重力加速度g=10m/s2,已知A、D端之间的距离为L=1.2m。求:
(1)物块与传送带Ⅰ间的动摩擦因数μ1;
(2)物块第1次回到D点时的速度;
(3)物块第几次回到D点时的速度达到最大,最大速度为多大?

(1)物块与传送带Ⅰ间的动摩擦因数μ1;
(2)物块第1次回到D点时的速度;
(3)物块第几次回到D点时的速度达到最大,最大速度为多大?
(1)0.25;(2)3m/s;(3)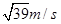
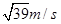
试题分析:(1)由题意可知,物块第一次到达A点时应满足:
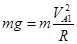
解得:
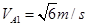 <V1
<V1故物块从D到A的过程中全程加速,由动能定理得:

代入数据解得:
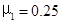 (5分)
(5分)(2)设物块第一次从B到C全程加速,则物块第一次由D经A、B到C的过程,由动能定理得:
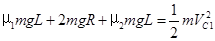
代入数据解得:
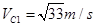 <V2
<V2故假设成立,则物块由D出发到第一次回到D的过程,由动能定理:

代入数据解得:
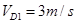 (5分)
(5分)(3)设每次物块在两传送带上都是全程加速,第N次到达C点时的速度恰好等于V2,
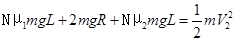
代入数据解得:N=4.4
同理,设第n次到达D点时的速度恰好等于V1,则由动能定理得:
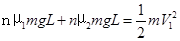
代入数据解得: n=4<N
故物块第4次到达C点时的速度小于传送带Ⅱ的速度V2,第4次到达D点时的速度恰好等于传送带Ⅰ的速度V1。则物块第4次到达D点后,同传送带Ⅰ一起匀速运动到A点,第5次回到D点速度为VD5,由动能定理有:
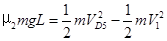
代入数据解得:
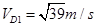
小物块第5次到达D点后,将沿传送带做减速运动,由于μ2<μ1,故物块在到达A点前必减速到与传送带相同的速度,以后每次到达D点的速度均为
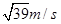 。
。综上所述,物块第5次经CD半圆形轨道到达D点时的速度达到最大,最大速度为
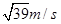 …(8分)
…(8分)
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

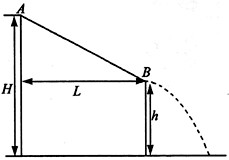

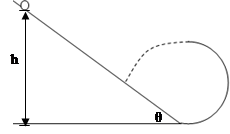
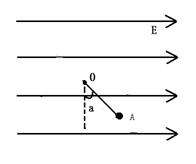
 的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求:
的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求:
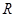 、
、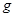 表示);
表示); 与
与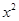 的关系如图所示,试求小球的质量和圆轨道半径。(
的关系如图所示,试求小球的质量和圆轨道半径。(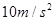 )
)