Question

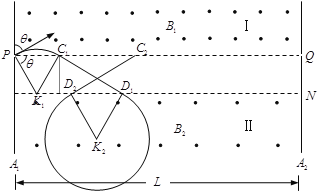
【题目】如图所示，足够大的平行挡板A1、A2竖直放置，间距为L。A1、A2上各有位置正对的小孔P、Q。两板间存在两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ，水平面PQ和MN分别是两个磁场区的理想边界面。挡板A1的左侧是方向水平向右的匀强电场，质量为m、电荷量为＋q的粒子从电场中的O点以大小为v0的初速度竖直向上射出，运动一段时间后从小孔P进入Ⅰ区，此时速度方向与竖直方向的夹角θ = 60。粒子进入Ⅰ区运动之后，从PQ边界上的 C1点第一次离开Ⅰ区，C1点与挡板A1的距离为d，然后进入没有磁场的区域运动，从MN边界上的D1点（图中未画出）第一次进入Ⅱ区，D1点与挡板A1的距离为。不计重力，碰到挡板的粒子不予考虑。

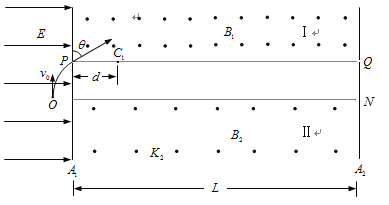
（1）求匀强电场中O、P两点间的电势差U和Ⅰ区的磁感应强度B1的大小；

（2）已知，最后粒子恰好从小孔Q射出，求Ⅱ区的磁感应强度B2的大小可能是哪些值？

Answer 1

【答案】（1）（2）、、

【解析】（1）粒子从O点运动到P点过程，由动能定理得

①

在P点速度满足

v0=vcosθ②

解得O、P两点间的电势差③

粒子在Ⅰ区内做圆周运动，有 ④

粒子运动情况如图，可得2r1cosθ=d⑤

解得Ⅰ区的磁感应强度⑥

（2）粒子在Ⅱ区内做圆周运动，有⑦

粒子运动情况如图，粒子完成一个完整的周期性运动，到达PQ边界的C2点时，与挡板A1的距离为 ⑧

即x=4d-r2

先不考虑粒子碰到挡板的情况下，恰好从小孔Q射出，有两种情况。

①第一种情况是粒子斜向下射出小孔Q，对应的条件是

Nx+d=L （n=1,2,3,……） ⑨

将L=13d代入并整理可得

⑩

考虑到r2>0，则n>3

再考虑粒子不能碰到挡板，则需满足条件 ⑾

可解得

综合以上条件，可知n只能取4和5两个值，即r2=d和r2=d⑿

解得Ⅱ区的磁感应强度大小的两个可能值是

和⒀

②第二种情况是粒子斜向上射出小孔Q，对应的条件是

nx=L （n=1,2,3,……） ⒁

可得 ⒂

考虑到r2>0，则n>3

粒子不能碰到挡板A2，需满足条件

⒃

解得r2<d

综合以上条件可知只能取n =4，即r2=d⒄

解得Ⅱ区的磁感应强度大小的另一个可能值是⒅