��Ŀ����
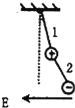
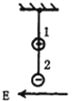
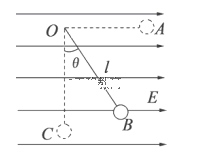
����Ŀ��.��ͼ��ʾ,����ˮƽ�������ǿ�糡����һ�̶���![]() ,��һ������Ϊ
,��һ������Ϊ![]() �ľ�Եϸ�߰�����Ϊ
�ľ�Եϸ�߰�����Ϊ![]() ,����
,����![]() ����ɵĽ���С��������
����ɵĽ���С��������![]() ��,С��ֹ��
��,С��ֹ��![]() ��ʱϸ������ֱ����ļн�Ϊ
��ʱϸ������ֱ����ļн�Ϊ![]() ,(
,(![]() ȡ10
ȡ10![]() ,
,![]() ,
,![]() ).��:
).��:
��1��![]() �����ĵ��Ʋ�
�����ĵ��Ʋ�![]() ;
;
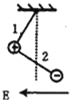
��2)��С������λ��![]() ʹϸ��ˮƽ���ɾ�ֹ�ͷ�,С��ͨ����͵�
ʹϸ��ˮƽ���ɾ�ֹ�ͷ�,С��ͨ����͵�![]() ʱϸ�߶�С�������
ʱϸ�߶�С�������![]() �Ĵ�С;
�Ĵ�С;
��3)���ҪʹС������![]() ����������Բ���˶�,��С����
����������Բ���˶�,��С����![]() ��ʱ�ش�ֱ��
��ʱ�ش�ֱ��![]() �����˶��ij��ٶ�
�����˶��ij��ٶ�![]() �Ĵ�С.
�Ĵ�С.
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
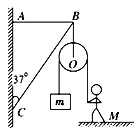
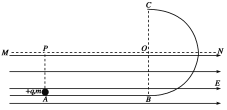
��1��С����B�㴦�ھ�ֹ״̬����С�������������������ƽ����������ǿ�糡�ij�ǿ����Ʋ��ϵ������⣻
��2����С���A���˶���C��Ĺ��������ö��ܶ������ɽ��⣻
��3����C�㣬С����������ϸ�ߵĺ����ṩ��������������������ʽ������⡣
��1������С����B�㾲ֹ����ƽ�⣬����ƽ����������qE=mgtan��
�ã�![]() ��2.5��103V/m
��2.5��103V/m
��U=Ed��UAB��EL(1sin��)��2.5��103��0.4��(1sin37��)��400V��
��2����С���˶���C��ʱ�ٶ�ΪvC����
mgL-qEL=![]() mvC2��
mvC2��
��ã�vC=1.4m/s��
��C�㣬С����������ϸ�ߵĺ����ṩ��������������������ʽ�ã�F-mg=m![]()
��������������ã�F=3N��
��3��С��������Բ���˶�ʱ����ͨ��B��ĶԳƵ㣬���ڸõ�ʱС�����С�ٶ�ΪV����mgcos��+qEsin�ȣ�![]()
mgLcos��qEL(1+sin��)��![]() mv2
mv2![]() mv02
mv02
������ã�v0��![]() m/s
m/s

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�