题目内容
2. 如图所示,一带电平行板电容器与水平方向成37°放置,下方有绝缘挡板支撑,板间距d=2.88cm,一带正电的小球的质量为0.02g,电荷量为10-7C,由电容器的中心A点静止释放恰好沿水平直线AB向右运动,从上极板边缘飞出进入边界BC右侧的水平向左的匀强电场区域,场强为2×l03V/m,经过一段时间后发现小球打在竖直挡板C点正下方的D处,(取g=10m/s2 )求:
如图所示,一带电平行板电容器与水平方向成37°放置,下方有绝缘挡板支撑,板间距d=2.88cm,一带正电的小球的质量为0.02g,电荷量为10-7C,由电容器的中心A点静止释放恰好沿水平直线AB向右运动,从上极板边缘飞出进入边界BC右侧的水平向左的匀强电场区域,场强为2×l03V/m,经过一段时间后发现小球打在竖直挡板C点正下方的D处,(取g=10m/s2 )求:(1)平行板电容器内的场强大小
(2)小球从上极板边缘飞出的速度
(3)CD间的距离.
分析 (1)在AB过程中受到的合力水平向右,故对小球受力分析,即可求得
(2)在AB过程中,根据动能定理求的速度
(3)在右侧电场中,小球在水平方向匀减速运动,竖直方向做自由落体运动,根据运动学公式即可求得
解答 解:(1)小球在平行板电容器中,根据受力分析可得qEcos37°=mg
解得E=$\frac{mg}{qcos37°}=\frac{0.02×1{0}^{-3}×10}{1{0}^{-7}×0.8}V/m=2500V/m$
(2)从A到B由动能定理可得
qE$•\frac{d}{2}=\frac{1}{2}m{v}^{2}$
解得v=$\sqrt{\frac{qEd}{m}}=\sqrt{\frac{1{0}^{-7}×2500×0.0288}{2×1{0}^{-5}}}m/s=0.6m/s$
(3)小球进入右侧电场后,小球在水平方向匀减速运动,竖直方向做自由落体运动,
在水平方向由牛顿第二定律可得qE′=ma
a=$\frac{qE′}{m}=\frac{1{0}^{-7}×2×1{0}^{3}}{2×1{0}^{-5}}m/{s}^{2}=10m/{s}^{2}$
水平减速到零所需时间为t=$\frac{v}{a}=\frac{0.6}{10}s=0.06s$
方向到达D点所需时间为t′=t=0.06s
故总时间为t总=t+t′=0.12s
在竖直方向通过的位移为h=$\frac{1}{2}{gt}_{总}^{2}=\frac{1}{2}×10×0.1{2}^{2}m=0.072m$
CD间的距离为$△h=h-\frac{d}{cos37°}=0.036m=3.6cm$
答:(1)平行板电容器内的场强大小为2500V/m
(2)小球从上极板边缘飞出的速度为0.6m/s
(3)CD间的距离为为3.6cm
点评 本题关键是先判断出物体的运动情况,然后根据受力分析和动能定理列式,关键是抓住小球在有侧电场中竖直方向的运动

 阅读快车系列答案
阅读快车系列答案 如图所示,竖直平面内放一直角杆MON,杆的水平部分粗糙,动摩擦因数μ=0.2,
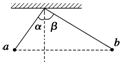
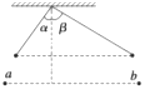
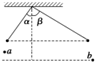
如图所示,竖直平面内放一直角杆MON,杆的水平部分粗糙,动摩擦因数μ=0.2,杆的竖直部分光滑.两部分各套有质量均为1kg的小球A和B,A、B球间用细绳相连.已知:OA=3m,OB=4m,若A球在水平拉力的作用下向右移动速度为2m/s时,B球的速度为( )
| A. | 1.5 m/s | B. | 3m/s | C. | 4 m/s | D. | $\frac{8}{3}$m/s |


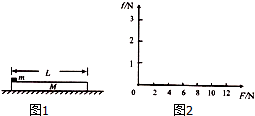 如图所示,质量M=2kg的木板静止在光滑的水平地面上,在木板的左端放置一个质量m=1kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ=0.2,取g=10m/s2,试求:
如图所示,质量M=2kg的木板静止在光滑的水平地面上,在木板的左端放置一个质量m=1kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ=0.2,取g=10m/s2,试求: