题目内容
（12分）如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道置于同一竖直平面上（R>r），两圆形轨道之间用一条水平粗糙轨道CD连接，轨道CD与甲乙两个圆形轨道相切于C、D两点。现有一小球以一定的速度先滑上甲轨道，绕行一圈后通过轨道CD再滑上乙轨道，绕行一圈后离开乙轨道。已知小球在甲轨道最高点处对轨道的压力等于球的重力，在乙轨道运动时恰好能过最高点。小球与轨道CD间的动摩擦系数为μ，求（1）小球过甲、乙轨道的最高点时的速度V1、 V2（2）水平CD段的长度L。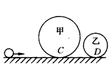 
解：设小球质量为m，当小球在甲轨道最高点时，
由牛顿第二定律得：N+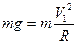
V1=" (2gR)" 1/2 （3分）
当小球在乙轨道最高点时，由牛顿第二定律得：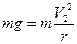
V2=" (gR)" 1/2 （3分）
小球从甲轨道最高点运动到乙轨道最高点的过程中，由动能定理得：
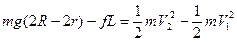（4分）
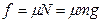（2分）
∴
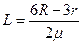
由牛顿第二定律得：N+
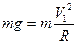
V1=" (2gR)" 1/2 （3分）
当小球在乙轨道最高点时，由牛顿第二定律得：
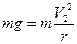
V2=" (gR)" 1/2 （3分）
小球从甲轨道最高点运动到乙轨道最高点的过程中，由动能定理得：
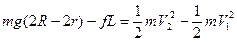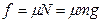（4分） （2分）∴
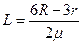
略
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
