题目内容
甲车以加速度3m/s2由静止开始作匀加速直线运动,乙车落后2s钟在同一地点由静止开始,以加速度4m/s2作匀加速直线运动,两车的运动方向相同,求:
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)最大距离是多少?
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)最大距离是多少?
解:(1)当甲乙两车速度相等时,两车距离最大
设:乙车经时间ts,则甲车经时间(t+2)s
则最大距离时有V甲=a甲(t+2)①
V乙=a乙t②
又由:V甲= V乙得:t=6s
(2)S甲=
S乙=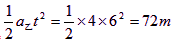
∴△S=S甲-S乙=24m。
设:乙车经时间ts,则甲车经时间(t+2)s
则最大距离时有V甲=a甲(t+2)①
V乙=a乙t②
又由:V甲= V乙得:t=6s
(2)S甲=

S乙=
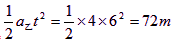
∴△S=S甲-S乙=24m。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目