题目内容
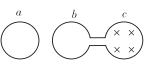
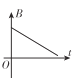
【题目】一端连在光滑固定轴上,可在竖直平面内自由转动的轻杆,另一端与一小球相连,如图甲所示。现使小球在竖直平面内做圆周运动,到达某一位置开始计时,取水平向右为正方向,小球的水平分速度 vx 随时间 t 的变化关系如图乙所示,不计空气阻力,下列说法中正确的是
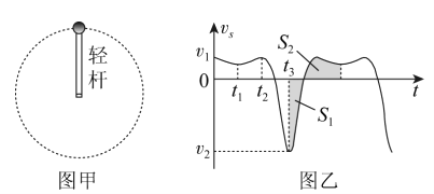
A.t1 时刻小球通过最高点,t3 时刻小球通过最低点
B.t2时刻小球通过最高点,t 3时刻小球通过最低点
C.v1 大小一定小于 v2 大小,图乙中 S1 和S 2 的面积一定相等
D.v1 大小可能等于 v2 大小,图乙中S 1 和S 2 的面积可能不等
【答案】AC
【解析】
AB.由对称性可知,在最高点左右两侧对称位置,小球沿水平方向分速度相同,那 么在小球达到最高点时,其前后对称时刻的小球的水平分速度相等且最高点时刻水平分速度为 正,在图乙中t1时刻满足要求,所以t1时刻小球通过最高点,同理t3时刻小球通过最低点。故 A正确B错误;
CD.从t2到t3,小球重力做正功,一直在加速,在最低点时,速度最大,沿水平 方向分速度也最大,即v2>v1,另外根据对运动过程分析可得S1和S2分别代表从最低点到最左 边点以及从最左边点到最高点的水平位移大小,它们对称相等,因此S1和S2的面积相等,故C 正确D错误。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目