题目内容
12. 如图所示,物体A的质量为2kg,与水平面间的动摩擦因数为0.3,水平拉力为5N,不计绳子与滑轮的摩擦和滑轮的质量,物体A获得的加速度a=2m/s2,在物体A移动0.4m的过程中,拉力F做功4J(g=10m/s2).
如图所示,物体A的质量为2kg,与水平面间的动摩擦因数为0.3,水平拉力为5N,不计绳子与滑轮的摩擦和滑轮的质量,物体A获得的加速度a=2m/s2,在物体A移动0.4m的过程中,拉力F做功4J(g=10m/s2).
分析 对A进行受力分析,根据牛顿第二定律求出加速度,先求出绳子运动的位移,再根据W=Fx即可求解.
解答 解:对A进行受力分析,根据牛顿第二定律得:
2F-μmg=ma
解得:a==2m/s2
在物体A移动0.4m的过程中,绳子运动的位移为:
x=2×0.4=0.8m,
则拉力F做功为:
W=Fx=5×0.8=4J
故答案为:2;4.
点评 功的计算中常用的方法有两种:一种直接利用功的公式;二是利用动能关系;若题目中为变力做功,则应用动能定理求解.

练习册系列答案
相关题目
20.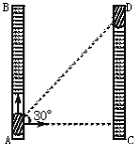 竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s的速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向成30°角,如图所示.若玻璃管的长度为1.0m,则可知玻璃管水平方向的移动速度和水平运动的距 离为( )
竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s的速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向成30°角,如图所示.若玻璃管的长度为1.0m,则可知玻璃管水平方向的移动速度和水平运动的距 离为( )
 竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s的速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向成30°角,如图所示.若玻璃管的长度为1.0m,则可知玻璃管水平方向的移动速度和水平运动的距 离为( )
竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s的速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向成30°角,如图所示.若玻璃管的长度为1.0m,则可知玻璃管水平方向的移动速度和水平运动的距 离为( )| A. | 0.1 m/s,1.7 m | B. | 0.17 m/s,1.0 m | C. | 0.17 m/s,1.7 m | D. | 0.1 m/s,1.0 m |
4.关于开普勒第三定律=K,以下理解正确的是( )
| A. | K是一个与行星无关的量 | |
| B. | T表示行星运动的自转周期 | |
| C. | T表示行星运动的公转周期 | |
| D. | 若地球绕太阳运转的半长轴为R地,周期为T地;月球绕地球运转的半长轴为r月,周期为t月,则= |
1.真空中两个点电荷的相互作用力大小为F,若将每个电荷的电量都加倍,同时使他们之间的距离减半,则他们间的相互作用力大小变为( )
| A. | 4F | B. | 2F | C. | 16F | D. | F |
2.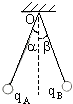 如图所示,用同样的细绳把两个质量相等的A、B小球悬挂在同一点O上,两球带同种电荷,且qA>qB,则下列关系式中正确的是( )
如图所示,用同样的细绳把两个质量相等的A、B小球悬挂在同一点O上,两球带同种电荷,且qA>qB,则下列关系式中正确的是( )
 如图所示,用同样的细绳把两个质量相等的A、B小球悬挂在同一点O上,两球带同种电荷,且qA>qB,则下列关系式中正确的是( )
如图所示,用同样的细绳把两个质量相等的A、B小球悬挂在同一点O上,两球带同种电荷,且qA>qB,则下列关系式中正确的是( )| A. | α>β | B. | α=β | ||
| C. | α<β | D. | 以上说法都不正确 |

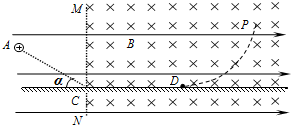 如图,空间内存在水平向右的匀强电场,在虚线MN的右侧有垂直纸面向里、磁感应强度为B的匀强磁场,一质量为m、带电荷量为+q的小颗粒自A点由静止开始运动,刚好沿直线运动至光滑绝缘的水平面C点,与水平面碰撞的瞬间小颗粒的竖直分速度立即减为零,而水平分速度不变,小颗粒运动至D处刚好离开水平面,然后沿图示曲线DP轨迹运动,AC与水平面夹角α=30°,重力加速度为g,求:
如图,空间内存在水平向右的匀强电场,在虚线MN的右侧有垂直纸面向里、磁感应强度为B的匀强磁场,一质量为m、带电荷量为+q的小颗粒自A点由静止开始运动,刚好沿直线运动至光滑绝缘的水平面C点,与水平面碰撞的瞬间小颗粒的竖直分速度立即减为零,而水平分速度不变,小颗粒运动至D处刚好离开水平面,然后沿图示曲线DP轨迹运动,AC与水平面夹角α=30°,重力加速度为g,求:



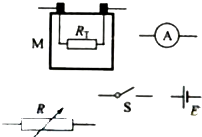 如图,一热敏电阻RT放在控温容器M内:
如图,一热敏电阻RT放在控温容器M内: 为毫安表,量程6mA,内阻为数十欧姆;E为直流电源,电动势约为3V,内阻很小;R为电阻箱,最大阻值为999.9Ω;S为开关.已知RT在95℃时阻值为150Ω,在20℃时的阻值约为550Ω.现要求在降温过程中测量在95℃~20℃之间的多个温度下RT的阻值.
为毫安表,量程6mA,内阻为数十欧姆;E为直流电源,电动势约为3V,内阻很小;R为电阻箱,最大阻值为999.9Ω;S为开关.已知RT在95℃时阻值为150Ω,在20℃时的阻值约为550Ω.现要求在降温过程中测量在95℃~20℃之间的多个温度下RT的阻值.