题目内容
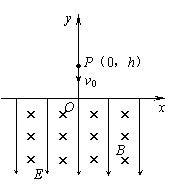
如图，坐标系xOy在竖直平面内，第一象限内分布匀强磁场，磁感应强度大小为B，方向垂直纸面向外；第二象限内分布着沿x轴正方向的水平匀强电场，场强大小E=| B2qL |
| 6m |
| ||
| 2 |
（1）带电粒子进入磁场时速度v的大小．
（2）P点与O点之间的距离．
分析：1、粒子在电场中只受电场力，粒子水平向右做匀加速直线运动，水平进入第一象限的磁场，在第二象限中根据动能定理计算带电粒子进入磁场时速度v的大小．
2、粒子在第一象限中，只受洛伦兹力，洛伦兹力提供向心力，粒子做圆周运动，计算出半径，画出轨迹，根据直角三角形的知识求解OP距离．
2、粒子在第一象限中，只受洛伦兹力，洛伦兹力提供向心力，粒子做圆周运动，计算出半径，画出轨迹，根据直角三角形的知识求解OP距离．
解答：解：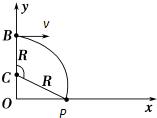
（1）设粒子进入磁场的速度为v，由动能定理得qEL=
mv2
又E=
解得：v=
（2）粒子在磁场中做匀速圆周运动，设半径为R．
由qvB=m
解得：R=
，
设圆心为C点，则CP=R=
，
OC=
L-R=
L
在直角三角形COP中，有勾股定理的OP=
L．
答：（1）带电粒子进入磁场时速度v的大小为
．
（2）P点与O点之间的距离为
L．
（1）设粒子进入磁场的速度为v，由动能定理得qEL=| 1 |
| 2 |
又E=
| B2qL |
| 6m |
解得：v=
| ||
| 3m |
（2）粒子在磁场中做匀速圆周运动，设半径为R．
由qvB=m
| v2 |
| R |
解得：R=
| ||
| 3 |
设圆心为C点，则CP=R=
| ||
| 3 |
OC=
| ||
| 2 |
| ||
| 6 |
在直角三角形COP中，有勾股定理的OP=
| 1 |
| 2 |
答：（1）带电粒子进入磁场时速度v的大小为
| ||
| 3m |
（2）P点与O点之间的距离为
| 1 |
| 2 |
点评：本题中带电小球先加速后做圆周运动，关键是画出轨迹图，结合几何关系进行分析．
练习册系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
，质量为m、电荷量为＋q的带电粒子从A点由静止释放，A点坐标为(-L ，
)，在静电力的作用下以一定速度进入磁场，最后落在x轴上的P点．不计粒子的重力．求：
，质量为m、电荷量为＋q的带电粒子从A点由静止释放，A点坐标为(-L ，
)，在静电力的作用下以一定速度进入磁场，最后落在x轴上的P点．不计粒子的重力．求：