题目内容
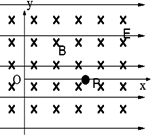
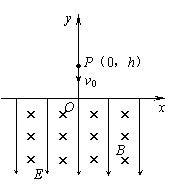
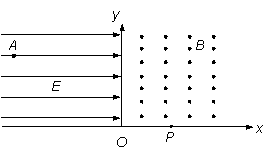
如图，坐标系xOy在竖直平面内，第一象限内分布匀强磁场，磁感应强度大小为B，方向垂直纸面向外；第二象限内分布着沿x轴正方向的水平匀强电场，场强大小
，质量为m、电荷量为＋q的带电粒子从A点由静止释放，A点坐标为(-L ，
)，在静电力的作用下以一定速度进入磁场，最后落在x轴上的P点．不计粒子的重力．求：
(1)带电粒子进入磁场时速度v的大小.
(2) P点与O点之间的距离.
(1)设粒子进入磁场的速度为v，由动能定理得
（2分） 又
解得：
（2分）
(2)粒子在磁场中做匀速圆周运动，设半径为R
由
（2分）
解得：
（2分）
设圆心为C点，则CP＝，（1分） OC＝
－R＝
（1分）
由几何关系解得P点到O点的距离为xOP＝
（2分）
说明：⑴没有必要的文字说明，没有设或没有说明依据的定理（公式），全题扣1分.
⑵把大写L写成小写l ，质量m写成M等该方程为0分..
 |
练习册系列答案
阅读快车系列答案
相关题目
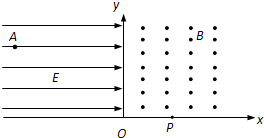如图，坐标系xOy在竖直平面内，第一象限内分布匀强磁场，磁感应强度大小为B，方向垂直纸面向外；第二象限内分布着沿x轴正方向的水平匀强电场，场强大小
，质量为m、电荷量为＋q的带电粒子从A点由静止释放，A点坐标为(-L ，
)，在静电力的作用下以一定速度进入磁场，最后落在x轴上的P点．不计粒子的重力．求：