题目内容
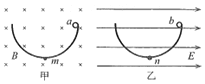
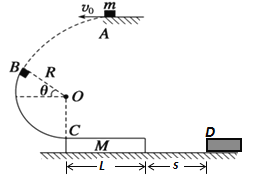
【题目】如图所示，阻值不计的足够长的光滑平行金属导轨水平放置，导轨左侧接一阻值R=0.4Ω的电阻，一质量m=1kg、电阻r=0.2Ω的金属棒MN置于导轨上，与导轨垂直且接触良好，整个装置处于垂直导轨平面向下的匀强磁场中。现对棒施加平彳于导轨的作用力F=0.6v+0.3（N）（v为棒运动速度），棒由静止开始运动，测得电阻两端电压随时间均匀增大。试回答以下问题：
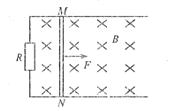
（1）分析并说明该棒在磁场中做何种性质的运动；
（2）求t=2s时棒的速度和棒两端的电压；
（3）求棒运动的前2s内流过电阻R的电荷量。
【答案】（1）该棒在磁场中做匀加速直线运动运动；（2）0.24V；（3）0.6C。
【解析】
（1）测得电阻两端电压随时间均匀增大，R两端电压U正比于电流I，感应电动势E正比于v，U随时间均匀增大，即V随时间均匀增大，加速度为恒量，所以金属棒做匀加速运动；
（2）对金属棒受力分析，由牛顿第二定律可知：
将F=0.6v+0.3带入得（0.6-
）v+0.3=ma，
因为a为定值，故0.6-=0，故BL=0.6Tm，a=0.3m/s2，
故t=2s时棒的速度v=at=0.6m/s；
此时的电动势
，
回路电流
，
导体棒两端电压UMN=IR
联立解得：UMN=0.24V；
（3）前2秒内导体棒移动的距离
，
根据电荷量的推论公式
=
；
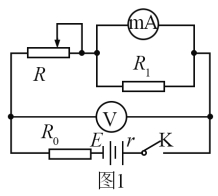
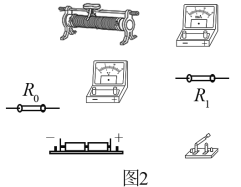
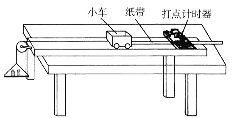
阅读快车系列答案
【题目】ab是一段粗细均匀的合金金属丝，为测定该金属丝的电阻率ρ，某实验小组设计了如图甲所示的电路。R0是阻值为2Ω的保护电阻，滑片P与电阻丝始终接触良好。
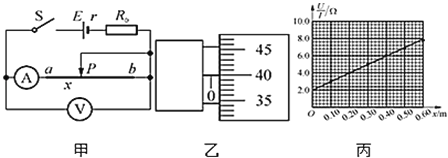
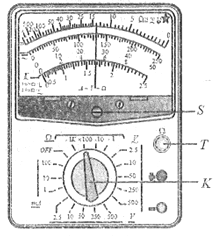
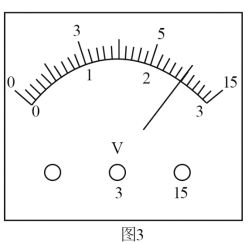
（1）实验中用螺旋测微器测得电阻丝的直径如图乙所示，其示数为d=____mm。
（2）实验时闭合开关，调节P的位置，记录aP长度x和对应的电压U、电流I等相关数据，如表：
x/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
U/V | 1.50 | 1.72 | 1.89 | 2.00 | 2.10 | 2.18 |
I/A | 0.49 | 0.43 | 0.38 | 0.33 | 0.31 | 0.28 |
| 3.06 | 4.00 | 4.97 | 6.06 | 6.77 | 7.79 |
若不考虑电流表的内阻，请利用题中所给字母写出该合金金属丝电阻率的表达式ρ=_____________ 。
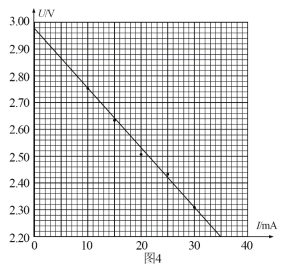
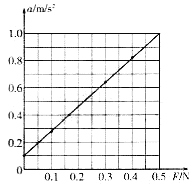
（3）据表中数据作出
﹣x关系如图丙所示，利用该图，可求得电阻丝的电阻率ρ为______Ωm（结果保留两位有效数字）。图丙中﹣x关系图线纵轴截距的物理意义是__________________。
