题目内容
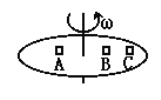
【题目】如图所示,甲、乙是竖直面内两个相同的半圆形光滑轨道,m、n为两轨道的最低点匀强滋场垂直于甲轨道平面,匀强电场平行于乙轨道平面。两个完全相同的带正电小球a、b分别从甲、乙两轨道的右侧最高点由静止释放,在它们第一次到达最低点的过程中,下列说法正确的是( )
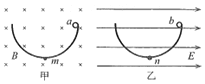
A. a球下滑的时间比b球下滑时间长B. a、b两球的机械能均不守恒
C. a球到m点的速度小于b球到n点的速度D. a球对m点的压力大于b球对n点的压力
【答案】D
【解析】
由于小球在磁场中运动,磁场力对小球不做功,整个过程中小球的机械能守恒;而小球在电场中运动受到的电场力对小球做负功,到达最低点时的速度的大小较小,所以在电场中运动的时间也长,故AC错误;磁场力对小球不做功,整个过程中小球a的机械能守恒;小球b在电场中运动受到的电场力对小球做负功,机械能减小,故B错误;小球在磁场中运动,在最低点进行受力分析可知:Fm-mg-Bqvm=m![]() ,解得:Fm=m
,解得:Fm=m![]() +mg+Bqvm …①
+mg+Bqvm …①
小球在电场中运动,在最低点受力分析可知:Fn-mg=m![]() ;解得:Fn=m
;解得:Fn=m![]() +mg …②
+mg …②
因为vm>vn,所以Fm>Fn,故D正确。故选D。

练习册系列答案
相关题目