题目内容
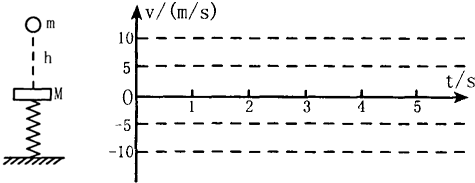
如图所示,一轻弹簧竖直放置在地面上,轻弹簧下端与地面固定,上端连接一质量为M的水平钢板,处于静止状态.现有一质量为 m 的小球从距钢板 h=5m的高处自由下落并与钢板发生碰撞,碰撞时间极短且无机械能损失.己知 M=3m,不计空气阻力,g=10m/s2.
( l )求小球与钢板第一次碰撞后瞬间,小球的速度 v1和钢板的速度 v2.
( 2 )如果钢板作简谐运动的周期为 2.0s,以小球自由下落的瞬间为计时起点,以向下方向为正方向,在下图中画出小球的速度 v 随时间 t 变化的v-t 图线.要求至少画出小球与钢板发生四次碰撞之前的图线.(不要求写出计算过程,只按画出的图线给分)
( l )求小球与钢板第一次碰撞后瞬间,小球的速度 v1和钢板的速度 v2.
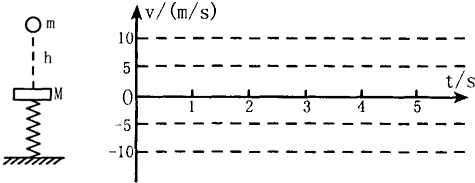
( 2 )如果钢板作简谐运动的周期为 2.0s,以小球自由下落的瞬间为计时起点,以向下方向为正方向,在下图中画出小球的速度 v 随时间 t 变化的v-t 图线.要求至少画出小球与钢板发生四次碰撞之前的图线.(不要求写出计算过程,只按画出的图线给分)

(1)设小球与钢板第一次碰撞前瞬时的速度大小v0,小球与钢板第一次碰撞后,小球与钢板的速度分别为v1和v2.取竖直向下方向为正方向.
由机械能守恒得:mgh=
mv
,解得,v0=
=10m/s
对于碰撞过程,由动量守恒和机械能守恒得:
mv0=mv1+Mv2 ①
m
=
m
+
M
②
又M=3m ③
联立①②③得:v1=-5m/s,v2=5m/s,即小球与钢板第一次碰撞后,小球的速度v1为 5m/s,方向向上;钢板的速度v2为 5m/s 方向向下.
( 2 )由上知,第一碰撞后小球作竖直上抛运动,总时间为t1=
=1s,而钢板作简谐运动的周期为T=2.0s,所以两者会在第一碰撞位置发生第二碰撞.
设第二次碰撞后,小球与钢板的速度分别为v1′和v2′.
由动量守恒和机械能守恒得:
mv1-Mv2=mv1′+Mv2 ′
m
+
M
=
m
+
M
又M=3m
联立以上三式解得,v1′=-10m/s,v2′=0.
此后小球竖直上抛运动,时间为t2=
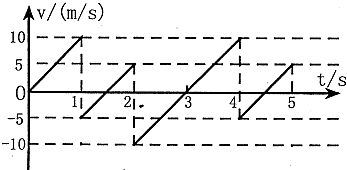
=2s=T,恰好经过2s后发生第三次碰撞,第三次碰撞与第一次碰撞相同.画出小球的v-t图线如下图所示(小球与钢板第二次碰撞后,小球的速度为 10m/s,方向向上;钢板的速度为零)
答:
(1)小球与钢板第一次碰撞后,小球的速度v1为 5m/s,方向向上;钢板的速度v2为 5m/s 方向向下.
(2)小球的v-t图线如图所示.
由机械能守恒得:mgh=
| 1 |
| 2 |
| 20 |
| 2gh |
对于碰撞过程,由动量守恒和机械能守恒得:
mv0=mv1+Mv2 ①
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
又M=3m ③
联立①②③得:v1=-5m/s,v2=5m/s,即小球与钢板第一次碰撞后,小球的速度v1为 5m/s,方向向上;钢板的速度v2为 5m/s 方向向下.
( 2 )由上知,第一碰撞后小球作竖直上抛运动,总时间为t1=
| 2v1 |
| g |
设第二次碰撞后,小球与钢板的速度分别为v1′和v2′.
由动量守恒和机械能守恒得:
mv1-Mv2=mv1′+Mv2 ′
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
| v | ′21 |
| 1 |
| 2 |
| v | ′22 |
又M=3m
联立以上三式解得,v1′=-10m/s,v2′=0.
此后小球竖直上抛运动,时间为t2=
| 2v′ |
| g |

答:
(1)小球与钢板第一次碰撞后,小球的速度v1为 5m/s,方向向上;钢板的速度v2为 5m/s 方向向下.
(2)小球的v-t图线如图所示.

练习册系列答案
相关题目
 如图所示,一轻弹簧竖直放置,下端固定在水平面上,上端处于a位置,一重球(可视为质点)无初速放在弹簧上端静止时,弹簧上端被压缩到b位置.现让重球从高于a位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩至d.不计空气阻力,以下关于重球在a至d的下落运动过程中的正确说法是:( )
如图所示,一轻弹簧竖直放置,下端固定在水平面上,上端处于a位置,一重球(可视为质点)无初速放在弹簧上端静止时,弹簧上端被压缩到b位置.现让重球从高于a位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩至d.不计空气阻力,以下关于重球在a至d的下落运动过程中的正确说法是:( ) (2009?湘潭一模)如图所示,一轻弹簧竖直放置,下端固定在水平面上,上端处于a位置,一重球(可视为质点)无初速放在弹簧上端静止时,弹簧上端被压缩到b位置.现让重球从高于a位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩至d,以下关于重球下落运动过程中的正确说法是(不计空气阻力)( )
(2009?湘潭一模)如图所示,一轻弹簧竖直放置,下端固定在水平面上,上端处于a位置,一重球(可视为质点)无初速放在弹簧上端静止时,弹簧上端被压缩到b位置.现让重球从高于a位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩至d,以下关于重球下落运动过程中的正确说法是(不计空气阻力)( ) 如图所示,一轻弹簧竖直固定在水平地面上,弹簧正上方有一个小球自由下落.从小球接触弹簧上端O点到将弹簧压缩到最短的过程中,小球的加速度a随时间t或者随距O 点的距离X变化的关系图线是( )
如图所示,一轻弹簧竖直固定在水平地面上,弹簧正上方有一个小球自由下落.从小球接触弹簧上端O点到将弹簧压缩到最短的过程中,小球的加速度a随时间t或者随距O 点的距离X变化的关系图线是( ) (A)如图所示,一轻弹簧竖直放置在地面上,下端固定,上端连接一质量为M的水平钢板,处于静止状态.现有一质量为m的小球从距钢板h=5m的高处自由下落并与钢板发生碰撞,碰撞后瞬间小球与钢板的速度大小相同.已知M=3m,不计空气阻力,重力加速度g取=10m/s2.则小球与钢板第一次碰撞后瞬间,钢板速度的大小为
(A)如图所示,一轻弹簧竖直放置在地面上,下端固定,上端连接一质量为M的水平钢板,处于静止状态.现有一质量为m的小球从距钢板h=5m的高处自由下落并与钢板发生碰撞,碰撞后瞬间小球与钢板的速度大小相同.已知M=3m,不计空气阻力,重力加速度g取=10m/s2.则小球与钢板第一次碰撞后瞬间,钢板速度的大小为