题目内容
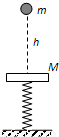
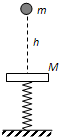（A）如图所示，一轻弹簧竖直放置在地面上，下端固定，上端连接一质量为M的水平钢板，处于静止状态．现有一质量为m的小球从距钢板h=5m的高处自由下落并与钢板发生碰撞，碰撞后瞬间小球与钢板的速度大小相同．已知M=3m，不计空气阻力，重力加速度g取=10m/s2．则小球与钢板第一次碰撞后瞬间，钢板速度的大小为（B）某星球的质量是地球的2倍，其半径是地球的
| 1 | 2 |
分析：（1）小球下落过程做自由落体运动，由运动学公式v=
求出小球与钢板碰撞前的速度大小．小球与钢板碰撞过程，系统动量守恒，求出第一次碰撞后瞬间钢板速度的大小，小球动量变化量△P=P′-P，等于碰撞前后动量之差．
（2）第一宇宙速度是卫星绕星近表面速度，根据地球对卫星的万有引力提供向心力求解．根据万有引力近似等于重力，求出重力之比．
| 2gh |
（2）第一宇宙速度是卫星绕星近表面速度，根据地球对卫星的万有引力提供向心力求解．根据万有引力近似等于重力，求出重力之比．
解答：解：（1）取竖直向下方向为正方向．
小球下落过程做自由落体运动，得小球与钢板碰撞前的速度大小v=
=
m/s=10m/s
小球与钢板碰撞过程，系统动量守恒，若碰撞后两者速度方向相同，则有mv=（M+m）v′，M=3m，解得，v′=2.5m/s，
即小球与钢板第一次碰撞后瞬间，钢板速度的大小为2.5m/s．
碰撞前后小球的动量变化量为△P=mv′-mv=m×2.5-m×10=-7.5m，即碰撞前后小球的动量变化量大小为7.5m．
若碰撞后两者速度方向相反，则
mv=-mv″+Mv″
解得，v″=5m，
△P=mv″-mv=-m×5-m×10=-15m，即碰撞前后小球的动量变化量大小为15m．
（2）设地球质量为M1，半径为R1；某星球的质量为M2，半径为R2
由万有引力定律得：G
=m
可得：第一宇宙速度v=
代入解得，该星球与地球第一宇宙速度之比为2：1．
故星球的第一宇宙速度是地球上第一宇宙速度的2倍．
由重力等于万有引力得：G重=G
则得：
=
?
=8
故答案为：A．2.5，7.5m或5，15 m；B．2；8
小球下落过程做自由落体运动，得小球与钢板碰撞前的速度大小v=
| 2gh |
| 2×10×5 |
小球与钢板碰撞过程，系统动量守恒，若碰撞后两者速度方向相同，则有mv=（M+m）v′，M=3m，解得，v′=2.5m/s，
即小球与钢板第一次碰撞后瞬间，钢板速度的大小为2.5m/s．
碰撞前后小球的动量变化量为△P=mv′-mv=m×2.5-m×10=-7.5m，即碰撞前后小球的动量变化量大小为7.5m．
若碰撞后两者速度方向相反，则
mv=-mv″+Mv″
解得，v″=5m，
△P=mv″-mv=-m×5-m×10=-15m，即碰撞前后小球的动量变化量大小为15m．
（2）设地球质量为M1，半径为R1；某星球的质量为M2，半径为R2
由万有引力定律得：G
| Mm |
| R2 |
| v2 |
| R |
可得：第一宇宙速度v=
|
代入解得，该星球与地球第一宇宙速度之比为2：1．
故星球的第一宇宙速度是地球上第一宇宙速度的2倍．
由重力等于万有引力得：G重=G
| Mm |
| R2 |
则得：
| G星 |
| G地 |
| M星 |
| M地 |
| ||
|
故答案为：A．2.5，7.5m或5，15 m；B．2；8
点评：对于卫星类型问题，关键是要建立物理模型，运用万有引力定律和向心力知识，加上数学变换来求解．
练习册系列答案
相关题目
如图所示，一轻弹簧竖直放置，下端固定在水平面上，上端处于a位置，一重球（可视为质点）无初速放在弹簧上端静止时，弹簧上端被压缩到b位置．现让重球从高于a位置的c位置沿弹簧中轴线自由下落，弹簧被重球压缩至d．不计空气阻力，以下关于重球在a至d的下落运动过程中的正确说法是：（ ）
如图所示，一轻质弹簧左端固定在长木块M的左端．右端与小物块m连接，且m与M及M与地面间光滑接触．开始时，m和M均静止，现同时对m、M施加等大反向的水平恒力F1和F2，使两物体开始运动，在弹簧由原长伸到最长的过程中，对m、M和弹簧组成的系统（整个过程中弹簧形变不超过其弹性限度，M足够长），下列说法正确的是（ ）
．若不计其他星球的影响，该星球的第一宇宙速度是地球上第一宇宙速度的 倍，某物体在该星球表面上所受重力是在地球表面上所受重力的 倍．