��Ŀ����
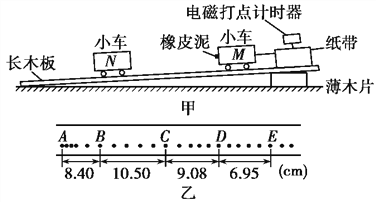
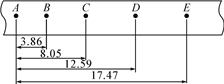
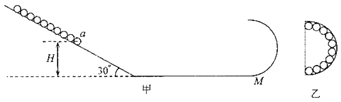
����Ŀ�����ͼ��ʾ���⻬�������������ɡ���������![]() ��б�棬�ұ��ǰ�Բ���м�Ϊ�㹻����ˮƽ�档б����ˮƽ��ƽ�����ӣ�ˮƽ�����Բ���У��е�ΪM������10����ͬ��С�뾶Ϊr������Ϊm����ЩС��ǡ��ռ���ұ�Բ���(����˵�����С��ǡ��ͬʱ��Բ���ֱ�����У�����ͼ��ʾ)����֪
��б�棬�ұ��ǰ�Բ���м�Ϊ�㹻����ˮƽ�档б����ˮƽ��ƽ�����ӣ�ˮƽ�����Բ���У��е�ΪM������10����ͬ��С�뾶Ϊr������Ϊm����ЩС��ǡ��ռ���ұ�Բ���(����˵�����С��ǡ��ͬʱ��Բ���ֱ�����У�����ͼ��ʾ)����֪![]() ���������ٶȴ�СΪg���ֽ�10��С�����η���б���ϣ��������С��a�����ľ�������ΪH�� ͬʱ�ͷ�����С�����
���������ٶȴ�СΪg���ֽ�10��С�����η���б���ϣ��������С��a�����ľ�������ΪH�� ͬʱ�ͷ�����С�����
����H��֪��aС��յ�ˮƽ��ʱ�����ʣ�
����H��֪��aС��յ�M��ʱ��Բ�����ѹ����
����aС���Բ�����ߵ��׳��������M�����L����HӦΪ���١�
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
�������������������1����aС��Ӿ�ֹ�˶���ˮƽ��Ĺ���Ӧ�û�е���غ���⣻��2���ɼ��ι�ϵ���Բ����뾶��Ȼ���aС����M��Ӧ��ţ�ٵڶ��������֧������������ţ�ٵ����������ѹ������3����ƽ���˶������������ߵ���ٶȣ�Ȼ���ɶ��ܶ�����⣮
��1�����ͷ�����С��aС��յ�ˮƽ�棬ѡ����Ϊ�ο�ƽ��
���ݻ�е���غ㶨���У� ![]()
��ã�aС��յ�ˮƽ��ʱ���ٶ�![]()
��2�����ͷ�����С��aС��M����ѡ����Ϊ�ο�ƽ�棬���ݻ�е���غ��У�
![]()
��ã� ![]()
��Բ����İ뾶ΪR���ɼ��ι�ϵ�ã� ![]()
��ã�Բ����뾶![]()
��M�㣬��ţ�ٵڶ����ɵã� ![]()
��ã� ![]()
��ţ�ٵ������ɿ�֪aС��յ�M��ʱ��Բ�����ѹ��Ϊ![]()
��3��aС����ƽ���˶�����ƽ��ˮƽ���ٶ�Ϊ![]() ����ƽ���˶����ɵã�
����ƽ���˶����ɵã�
��ֱ�����У� ![]()
ˮƽ�����У� ![]()
�����ã� ![]()
���ͷ�����С��aС��ﵽ��ߵ㣬ѡ����Ϊ�ο�ƽ�棬���ݻ�е���غ��У�
![]()
��ã� ![]()