题目内容
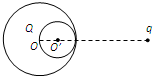 如图半径为R的大球O被内切地挖去半径为
如图半径为R的大球O被内切地挖去半径为| R |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:运用割补的思想,讨论电荷间的作用力,当没有挖去小球时整个大球带有电荷8Q,求出此时与点电荷q间的相互作用力,再求出挖去的小球与q的相互作用力,根据力的合成可知,两者之差即为挖去小球后的作用力.
解答:解:先求出整个大球与挖去小球的体积关系,由于挖去小球均匀地带有电荷量Q,所以可以求得原来大球带有的电荷量为8Q,则此时大球与点电荷间的作用力为
,挖去的小球球心离点电荷q距离为r-
,小球带电荷量为Q,则小球与点电荷间的作用力为
,原先大球与点电荷的作用力为
,现挖去一小球后减小的作用力为
,故大球余下部分与点电荷间的作用力为两者之差即为:
-
,整理可得C选项正确.
故选:C
| k8Qq |
| r2 |
| R |
| 2 |
| kQq | ||
(r-
|
| k8Qq |
| r2 |
| kQq | ||
(r-
|
| k8Qq |
| r2 |
| kQq | ||
(r-
|
故选:C
点评:根据库仑定律,巧用割补法思想根据力的合成求解是解决本题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
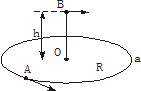 如图所示,小球A在光滑的半径为R的圆形槽内做匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿Oa方向以某一初速水平抛出,结果恰好在a点与A球相碰.求:(1)B球抛出时的水平初速多大?
如图所示,小球A在光滑的半径为R的圆形槽内做匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿Oa方向以某一初速水平抛出,结果恰好在a点与A球相碰.求:(1)B球抛出时的水平初速多大?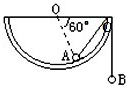 如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.
如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.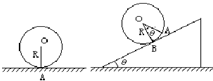 如图所示,有一个半径为R的圆球,其重心不在球心O上,现将它置于水平地面上,则有平衡时球与地面的接触点为A,若将它置于倾角为θ的粗糙斜面上,则平衡时(静摩擦力足够大)球与斜面的接触点为B,已知AB的圆心角为θ,求圆球的重心离球心的距离是
如图所示,有一个半径为R的圆球,其重心不在球心O上,现将它置于水平地面上,则有平衡时球与地面的接触点为A,若将它置于倾角为θ的粗糙斜面上,则平衡时(静摩擦力足够大)球与斜面的接触点为B,已知AB的圆心角为θ,求圆球的重心离球心的距离是





















