题目内容
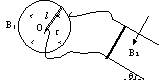
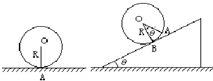 如图所示,有一个半径为R的圆球,其重心不在球心O上,现将它置于水平地面上,则有平衡时球与地面的接触点为A,若将它置于倾角为θ的粗糙斜面上,则平衡时(静摩擦力足够大)球与斜面的接触点为B,已知AB的圆心角为θ,求圆球的重心离球心的距离是
如图所示,有一个半径为R的圆球,其重心不在球心O上,现将它置于水平地面上,则有平衡时球与地面的接触点为A,若将它置于倾角为θ的粗糙斜面上,则平衡时(静摩擦力足够大)球与斜面的接触点为B,已知AB的圆心角为θ,求圆球的重心离球心的距离是分析:在图A中,球受重力和支持力,二力平衡,故重力的作用点在OA连线上的某个点;在图B中,以B点为支点,根据力矩平衡条件,合力的力矩为零,故重力的力矩一定为零,故重心也在过B的竖直线上,一定是该线与OA的交点.
解答:解:在图A中,球受重力和支持力,二力平衡,故重力的作用点在OA连线上;
在图B中,以B点为支点,根据力矩平衡条件,合力的力矩为零,故重力的力矩一定为零,故重心也在过B的竖直线上,一定是该线与OA的交点,如图所示:
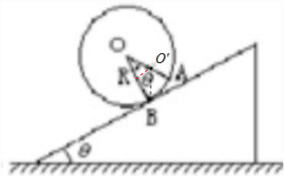
结合几何关系,有:
R=2×(AO′)?cosθ
解得:AO′=
故答案为:
.
在图B中,以B点为支点,根据力矩平衡条件,合力的力矩为零,故重力的力矩一定为零,故重心也在过B的竖直线上,一定是该线与OA的交点,如图所示:

结合几何关系,有:
R=2×(AO′)?cosθ
解得:AO′=
| R |
| 2cosθ |
故答案为:
| R |
| 2cosθ |
点评:重心是重力的作用点,本题关键结合共点力平衡条件和力矩平衡条件判断出重心的位置,然后结合几何关系列式求解,不难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
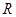 的圆弧形的轨道,滑块
的圆弧形的轨道,滑块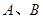 分别从轨
道上面和下面沿轨道滑动,如果要求它们在最高处不离开轨道,对它们在最高点的速率有什么限制?
分别从轨
道上面和下面沿轨道滑动,如果要求它们在最高处不离开轨道,对它们在最高点的速率有什么限制?
 沿轨道滑动,如果要求它们在最高处不离开轨道,对它们在最高
沿轨道滑动,如果要求它们在最高处不离开轨道,对它们在最高 点的速率有什么限制?
点的速率有什么限制?