题目内容
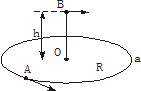 如图所示,小球A在光滑的半径为R的圆形槽内做匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿Oa方向以某一初速水平抛出,结果恰好在a点与A球相碰.求:(1)B球抛出时的水平初速多大?
如图所示,小球A在光滑的半径为R的圆形槽内做匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿Oa方向以某一初速水平抛出,结果恰好在a点与A球相碰.求:(1)B球抛出时的水平初速多大?(2)A球速度满足什么条件,两球就能在a点相碰?
分析:(1)平抛运动的高度决定运动的时间,根据h=
gt2 求出运动的时间,根据水平方向做匀速直线运动求出B球平抛的初速度.
(2)平抛运动的时间一定,两球相碰,则运动的时间相等,考虑到A球运动周期性,根据
=
求出A球的速度.
| 1 |
| 2 |
(2)平抛运动的时间一定,两球相碰,则运动的时间相等,考虑到A球运动周期性,根据
| 2kπR |
| v |
|
解答:解:(1)由h=
gt2
R=v0t 解得B球的水平初速v0=R
.
(2)B球下落的时间t=
.
只要在B球落至a点时A球同时也到达a点即相碰.考虑到A球运动的周期性,
所以有
=
,
由此解得v=2kπR
(k=1,2,3,…).
| 1 |
| 2 |
R=v0t 解得B球的水平初速v0=R
|
(2)B球下落的时间t=
|
只要在B球落至a点时A球同时也到达a点即相碰.考虑到A球运动的周期性,
所以有
| 2kπR |
| v |
|
由此解得v=2kπR
|
点评:解决本题的关键知道平抛运动的时间由高度决定,两球相遇,时间相等,注意A球运动的周期性.

练习册系列答案
相关题目
 (选修3-5)
(选修3-5)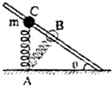 如图所示,固定的倾斜光滑杆上套有一个质量为m的小球,小球与一轻质弹簧一端相连,弹簧的另一端固定在地面上的A点,已知杆与水平面之间的夹角θ<45°,当小球位于B点时,弹簧与杆垂直,此时弹簧处于原长.现让小球自C点由静止释放,在小球滑到杆底端的整个过程中,关于小球的动能、重力势能和弹簧的弹性势能,下列说法正确的是( )
如图所示,固定的倾斜光滑杆上套有一个质量为m的小球,小球与一轻质弹簧一端相连,弹簧的另一端固定在地面上的A点,已知杆与水平面之间的夹角θ<45°,当小球位于B点时,弹簧与杆垂直,此时弹簧处于原长.现让小球自C点由静止释放,在小球滑到杆底端的整个过程中,关于小球的动能、重力势能和弹簧的弹性势能,下列说法正确的是( )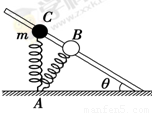
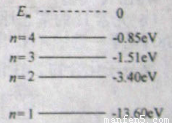
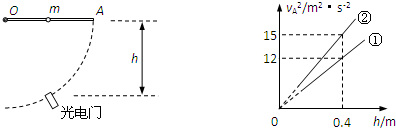
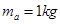 ,则b球的质量
,则b球的质量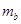 等于多少?
等于多少?