题目内容
【题目】如图所示,曲线I是一颗绕地球做圆周运动卫星轨道的示意图,其半径为R;曲线II是一颗绕地球椭圆运动卫星轨道的示意图,O点为地球球心,,AB为椭圆的长轴,两轨道和地心都在同一平面内,已知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是( )
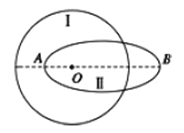
A. 椭圆轨道的长轴长度为R
B. 卫星在I 轨道的速率为v0,卫星在II轨道B点的速率为vB,则![]()
C. 卫星在I轨道的加速度大小为a0,卫星在II轨道A点加速度大小为aA,则![]()
D. 若OA=0.5R,则卫星在B点的速率![]()
【答案】BC
【解析】A项,根据开普勒第三定律可知椭圆轨道半长轴的立方与周期的平方之比是一个常数,由于两轨道上运动的卫星周期相等,所以轨道Ⅰ的半径和轨道Ⅱ的半长轴相等,所以AB的长度为2R,故A项错误。
B项,设两轨道的靠下的交点为C,在此点两个卫星受到的向心力大小相等,轨道I的万有引力提供了向心力,而轨道II是椭圆所以万有引力的一部分提供了向心力,根据![]() 知在此点,轨道I上的速度大于轨道II上的速度,在轨道II上从C点运动到B点做离心运动,万有引力做负功,所以动能减小,速度减小,所以
知在此点,轨道I上的速度大于轨道II上的速度,在轨道II上从C点运动到B点做离心运动,万有引力做负功,所以动能减小,速度减小,所以![]() ,故B正确;
,故B正确;
C项,两卫星都是由万有引力提供向心力,根据![]() 可知离地心越远,加速度越小,卫星1离地心的距离比卫星2在A点离地心的距离远,所以有
可知离地心越远,加速度越小,卫星1离地心的距离比卫星2在A点离地心的距离远,所以有![]() ,故C项正确。
,故C项正确。
D项,由A项分析可知AB=2R,因为OA=0.5R,所以OB=1.5R,设绕地球做匀速圆周运动,且半径为1.5R的卫星的速度为v,则有![]() ,根据万有引力提供向心力有
,根据万有引力提供向心力有![]() ,解得
,解得![]() ,所以
,所以![]() ,故D错误;
,故D错误;
故选BC
【题型】多选题
【结束】
7
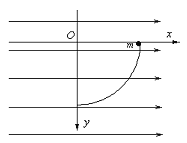
【题目】如图所示,半径为R的半圆形区域内分布着垂直纸面向里的匀强磁场,磁感应强度为B,半圆的左边垂直x轴放置一粒子发射装置,在-R≤y≤R的区间内各处均沿x轴正方向同时发射出一个带正电粒子,粒子质量均为m、电荷量均为q、初速度均为v,重力及粒子间的相互作用均忽略不计,所有粒子都能到达y轴,其中最后到达y轴的粒子比最先到达y轴的粒子晚△t时间,
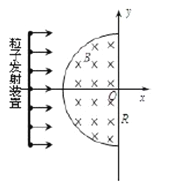
A. 磁场区域半径R应满足![]()
B. 有些粒子可能到达y轴上相同的位置
C. ![]() ,其中角度θ的弧度值满足
,其中角度θ的弧度值满足![]()
D. ![]()
【答案】BC
【解析】粒子在磁场中的运动图像如图:
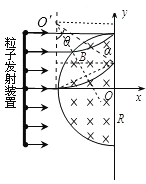
A项,如图,若沿x轴入射磁场的粒子要打到y轴上,要求粒子在磁场中的运动半径![]() ,故A项错误。
,故A项错误。
B项,由图可知,发生偏转的粒子也有可能打在y=R的位置上,故B正确
C、D项,只考虑![]() 方向分运动,在磁场中粒子做匀速圆周运动,速率不变,速度方向偏转,所以在磁场中运动路程越长,打到y轴所需时间越长,
方向分运动,在磁场中粒子做匀速圆周运动,速率不变,速度方向偏转,所以在磁场中运动路程越长,打到y轴所需时间越长,![]() ,即沿x轴入射磁场的粒子最后到达y轴,而
,即沿x轴入射磁场的粒子最后到达y轴,而![]() 处的粒子最先到达y轴,所需时间
处的粒子最先到达y轴,所需时间![]() ,所以
,所以![]() ,如图几何关系
,如图几何关系![]() ,故C项正确,D项错误。
,故C项正确,D项错误。
故选BC