题目内容
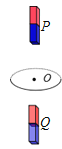
【题目】如图所示，两竖直固定且正对放置的导热气缸内被活塞各封闭一定质量的理想气体，活塞a、b用刚性轻杆相连，上下两活塞的横截面积Sa∶Sb＝1∶2，活塞处于平衡状态时，A、B中气体的体积均为V0，温度均为300 K，B中气体压强为0.75P0，P0为大气压强（两活塞及杆质量不计，活塞与气缸内壁间摩擦不计）。
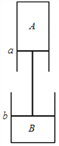
（i）求A中气体的压强；
（ii）现对B中气体加热，同时保持A中气体温度不变，活塞重新达到平衡状态后，A中气体的压强为P0，求此时B中气体的温度。
【答案】（i） PA＝0.5P0 （ii）T＝800 K
【解析】（i）以活塞为研究对象，根据受力情况有： 
将
， 
，代入解得： 
；
（ii）加热后A、B中气体压强均为
，则
对A中气体，根据玻意耳定律有： 
对B中气体，根据理想气体状态方程： 
解得： 
练习册系列答案
相关题目
