题目内容
一个质量为0.3kg的弹性小球，在光滑水平面上以6m/s的速度垂直撞到墙上，碰撞后小球沿相反方向运动，反弹后的速度大小与碰撞前相同。则碰撞前后小球速度变化量的大小为Δv和碰撞过程中墙对小球做功的大小W为
- A.Δv=0
- B.Δv=12m/s
- C.W=0
- D.W=10.8J
BC
试题分析：规定初速度方向为正方向，初速度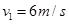
，碰撞后速度
，
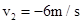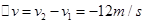，负号表示速度变化量的方向与初速度方向相反，所以碰撞前后小球速度变化量的大小为12m/s．故A错误．故B正确．运用动能定理研究碰撞过程，由于初、末动能相等，所以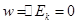
碰撞过程中墙对小球做功的大小W为0．故C正确．D错误．
故选BC．
考点：动能定理的应用；运动的合成和分解．
点评：对于矢量的加减，我们要考虑方向，动能定理是一个标量等式，对于动能定理的研究，则无需考虑方向．
试题分析：规定初速度方向为正方向，初速度
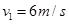，碰撞后速度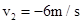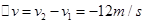，，负号表示速度变化量的方向与初速度方向相反，所以碰撞前后小球速度变化量的大小为12m/s．故A错误．故B正确．运用动能定理研究碰撞过程，由于初、末动能相等，所以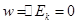碰撞过程中墙对小球做功的大小W为0．故C正确．D错误．
故选BC．
考点：动能定理的应用；运动的合成和分解．
点评：对于矢量的加减，我们要考虑方向，动能定理是一个标量等式，对于动能定理的研究，则无需考虑方向．
练习册系列答案
名校课堂系列答案
相关题目
一棵树上有一个质量为0.3kg的熟透了的苹果P，该苹果从树上A先落到地面C最后滚入沟底D．已知AC、CD的高度差分别为2.2m和3m，以地面C为零势能面，A、B、C、D、E面之间竖直距离如图所示．算出该苹果从A落下到D的过程中重力势能的减少量和在D处的重力势能分别是（ ）
一个质量为0.3kg的物体沿水平面做直线运动，如图所示，图线a表示物体受水平拉力时的 v-t 图象，图线b表示撤去水平拉力后物体继续运动的 v-t 图象，g=10m/s2，下列说法中正确的是（ ）一个质量为0.3kg的小球，在光滑水平面上以6m/s的速度垂直撞到墙上，碰撞后小球沿相反方向运动，反弹后的速度大小为4m/s．则碰撞前后墙对小球的冲量大小I及碰撞过程中墙对小球做的功W分别为（ ）
| A、I=3 kg?m/s W=-3J | B、I=0.6 kg?m/s W=-3J | C、I=3 kg?m/s W=7.8J | D、I=0.6 kg?m/s W=3J |