题目内容
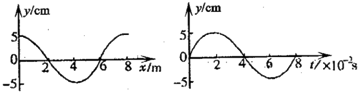
 一列沿x轴传播的横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.求:
一列沿x轴传播的横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.求:(1)波速多大?
(2)若2T>t2-t1>T,波速又为多大?
(3)若t2-t1>T,并且波速为3600m/s,则波沿哪个方向传播?
分析:(1)因为题中没有给出波的传播方向,故需要对波沿x轴正方向和x轴负方向传播分别进行讨论.又因为题中没有给出△t=t2-t1与周期T的关系,故需要考虑到波的重复性.运用波形平移法得出波的传播距离s与波长的关系,由v=
求得波速.
(2)波的一个周期内传播的距离是λ,当2T>t2-t1>T时,可知2λ>s>λ,根据上题结果分析求解本题.
(3)由s=vt求出波的传播距离,分析与波长的关系,即可判断波的传播方向.
| s |
| t |
(2)波的一个周期内传播的距离是λ,当2T>t2-t1>T时,可知2λ>s>λ,根据上题结果分析求解本题.
(3)由s=vt求出波的传播距离,分析与波长的关系,即可判断波的传播方向.
解答:解:(1)若波沿x轴正方向传播,则可看出是波形传播的最小距离 s0=
λ=2m
波传播的可能距离是s=s0+nλ=8n+2(m)
则可能的波速为v=
=
=1600n+400(m/s),(n=0、1、2、…)
若波沿x轴负方向传播,则可看出是波形传播的最小距离s0=
λ=6m
波传播的可能距离是s=s0+nλ=8n+6(m)
则可能的波速为v=
=
=1600n+1200(m/s),(n=0、1、2…)
(2)当2T>t2-t1>T时,根据波动与振动的对应性可知2λ>s>λ,这时波速的通解表达式中n=1.
若波沿x轴正方向传播,则波速为v=1600n+400=2000(m/s)
若波沿x轴负方向传播,则波速为v=1600n+1200=2800(m/s)
(3)当t2-t1>T,波速为3600m/s时,根据波动与振动的相应性可知t2-t1>T,
所以波向前传播的距离大于波长s>λ,而且可以计算出
s=vt=3600×0.005=18(m)
由于波长等于8m,这样波向前传播了
=
=2
个波长.由波形图不难判断出波是沿x轴向右传播的.
答:
(1)若波沿x轴正方向传播,波速是1600n+400(m/s),(n=0、1、2、…);若波沿x轴负方向传播,波速是1600n+1200(m/s),(n=0、1、2…).
(2)若2T>t2-t1>T,若波沿x轴正方向传播,波速为2000(m/s);若波沿x轴负方向传播,波速为2800(m/s).
(3)若t2-t1>T,并且波速为3600m/s,波沿x轴向右传播的.
| 1 |
| 4 |
波传播的可能距离是s=s0+nλ=8n+2(m)
则可能的波速为v=
| s |
| t |
| 8n+2 |
| 0.005 |
若波沿x轴负方向传播,则可看出是波形传播的最小距离s0=
| 3 |
| 4 |
波传播的可能距离是s=s0+nλ=8n+6(m)
则可能的波速为v=
| s |
| t |
| 8n+6 |
| 0.005 |
(2)当2T>t2-t1>T时,根据波动与振动的对应性可知2λ>s>λ,这时波速的通解表达式中n=1.
若波沿x轴正方向传播,则波速为v=1600n+400=2000(m/s)
若波沿x轴负方向传播,则波速为v=1600n+1200=2800(m/s)
(3)当t2-t1>T,波速为3600m/s时,根据波动与振动的相应性可知t2-t1>T,
所以波向前传播的距离大于波长s>λ,而且可以计算出
s=vt=3600×0.005=18(m)
由于波长等于8m,这样波向前传播了
| s |
| λ |
| 18 |
| 8 |
| 1 |
| 4 |
答:
(1)若波沿x轴正方向传播,波速是1600n+400(m/s),(n=0、1、2、…);若波沿x轴负方向传播,波速是1600n+1200(m/s),(n=0、1、2…).
(2)若2T>t2-t1>T,若波沿x轴正方向传播,波速为2000(m/s);若波沿x轴负方向传播,波速为2800(m/s).
(3)若t2-t1>T,并且波速为3600m/s,波沿x轴向右传播的.
点评:本题关键抓住波的周期性和双向性,运用波形的平移法进行分析和求解,是典型的多解问题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 一列沿x轴传播的横波,在t s与(t+0.4)s位于区间[-3m,3m]内的波形相同,如图所示,那么可以断定( )
一列沿x轴传播的横波,在t s与(t+0.4)s位于区间[-3m,3m]内的波形相同,如图所示,那么可以断定( ) (2010?奉贤区二模)一列沿x轴传播的横波,t与(t+0.4s)在-3m-3m的区间内的波形均如图所示,那么可以断定( )
(2010?奉贤区二模)一列沿x轴传播的横波,t与(t+0.4s)在-3m-3m的区间内的波形均如图所示,那么可以断定( )