题目内容
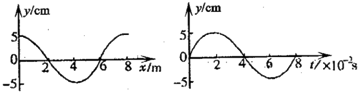
 一列沿x轴传播的横波,在t s与(t+0.4)s位于区间[-3m,3m]内的波形相同,如图所示,那么可以断定( )
一列沿x轴传播的横波,在t s与(t+0.4)s位于区间[-3m,3m]内的波形相同,如图所示,那么可以断定( )分析:由图读出波长.根据波的周期性,确定时间与周期的关系,确定出周期的可能值,求出最大周期和最大波速.
解答:解:
A、B由两个时刻的图象重合说明时间0.4s恰好是周期的整数倍,故应为nT=0.4s,n=1,2…,周期T=
s,波速为v=
=
m/s=10nm/s,则得到该波的最大周期为0.4s,最小波速v=10m/s,故A错误,B正确;
C、(t+0.2s)时,若周期T=
s,则x=3m的质点位移始终为零.故C正确.
D、由于无法判断x=3m处质点是不是波最前列的点,则不能确定各质点刚开始振动的方向.故D错误.
故选BC
A、B由两个时刻的图象重合说明时间0.4s恰好是周期的整数倍,故应为nT=0.4s,n=1,2…,周期T=
| 0.4 |
| n |
| λ |
| T |
| 4n |
| 0.4 |
C、(t+0.2s)时,若周期T=
| 0.4 |
| n |
D、由于无法判断x=3m处质点是不是波最前列的点,则不能确定各质点刚开始振动的方向.故D错误.
故选BC
点评:本题要注意两个时刻波形重合说明的是这段时间应是周期的整数倍,不能认为恰好是一个周期.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 (2010?奉贤区二模)一列沿x轴传播的横波,t与(t+0.4s)在-3m-3m的区间内的波形均如图所示,那么可以断定( )
(2010?奉贤区二模)一列沿x轴传播的横波,t与(t+0.4s)在-3m-3m的区间内的波形均如图所示,那么可以断定( ) 一列沿x轴传播的横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.求:
一列沿x轴传播的横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.求: