题目内容
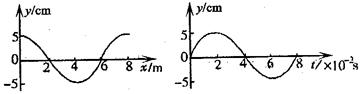
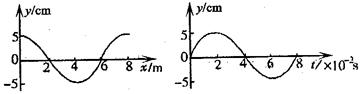
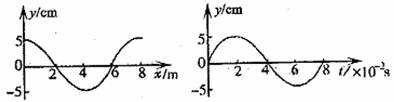
如图所示分别为一列沿x轴传播的横波在零时刻的图象和在x=6m处的质点从该时刻开始计时的振动图象.求:
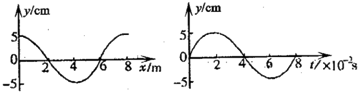
①该横波的传播方向和速度的大小
②x=6m处的质点位移随时间变化的关系式.

①该横波的传播方向和速度的大小
②x=6m处的质点位移随时间变化的关系式.
分析:①根据t=0时刻x=6m处质点的振动方向得到波的传播方向,由左图得到波长,右图得到周期,根据v=
求解波速.
②根据质点振动方程:y=Asinωt写出质点位移随时间变化的关系式.
| λ |
| T |
②根据质点振动方程:y=Asinωt写出质点位移随时间变化的关系式.
解答:解:①t=0时刻x=6m处质点的振动方向是向上,由波形平移法知,波沿x轴负方向传播;
由左图得到波长为λ=8m,右图得到周期为T=0.08s,故波速v=
=
=100m/s;
②由x=6m处的质点位移随时间变化的图象知为正弦函数,故关系式:y=0.05sin25πt;
答:①该横波的传播方向为x轴负方向,速度的大小为100m/s;
②x=6m处的质点位移随时间变化的关系式y=0.05sin25πt.
由左图得到波长为λ=8m,右图得到周期为T=0.08s,故波速v=
| λ |
| T |
| 8 |
| 0.08 |
②由x=6m处的质点位移随时间变化的图象知为正弦函数,故关系式:y=0.05sin25πt;
答:①该横波的传播方向为x轴负方向,速度的大小为100m/s;
②x=6m处的质点位移随时间变化的关系式y=0.05sin25πt.
点评:本题关键明确波形平移方向与质点振动方向的关系,能够结合公式v=
求解波速.
| λ |
| T |

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目