题目内容
如图所示，一轻质细绳绕过定滑轮，一端连接一置于水平地面上的物块B，另一端连接劲度系数为k的轻质弹簧，弹簧下端悬挂着质量为m的物块A，物块A带有+q的电荷，整个装置处在竖直向下，场强为E=
的匀强电场中。现让A从弹簧原长的位置静止释放，使A在竖直方向上做简谐运动，当A运动到最低点时，B刚要离开地面。不计滑轮的摩擦，弹簧在弹性限度内，m、g、k、q为已知量。求：
（1）物块A运动到最低点时的加速度a；
（2）物块B的质量M；
（3）在以后的运动过程中弹簧的最大弹性势能Ep。
的匀强电场中。现让A从弹簧原长的位置静止释放，使A在竖直方向上做简谐运动，当A运动到最低点时，B刚要离开地面。不计滑轮的摩擦，弹簧在弹性限度内，m、g、k、q为已知量。求：（1）物块A运动到最低点时的加速度a；
（2）物块B的质量M；
（3）在以后的运动过程中弹簧的最大弹性势能Ep。
解：（1）设物块A刚释放时，加速度为a1，有Eq+mg=ma1 ①
由简谐运动的对称性可知，a= a1 ②
得：a=2g ③，方向竖直向上④
（2）在最低点，设弹力为F，有F－Eq－mg=ma ⑤
当B刚要离开地面时，有：F=Mg ⑥
联立③⑤⑥解得，M= 4m ⑦
（3）当A运动到平衡位置时，设弹簧的形变量为x0，有：mg+qE =kx0 ⑧
A从最高点到最低点，由功能关系得2mgx0+2qEx0= Ep ⑨
解得Ep=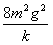
⑩
由简谐运动的对称性可知，a= a1 ②
得：a=2g ③，方向竖直向上④
（2）在最低点，设弹力为F，有F－Eq－mg=ma ⑤
当B刚要离开地面时，有：F=Mg ⑥
联立③⑤⑥解得，M= 4m ⑦
（3）当A运动到平衡位置时，设弹簧的形变量为x0，有：mg+qE =kx0 ⑧
A从最高点到最低点，由功能关系得2mgx0+2qEx0= Ep ⑨
解得Ep=
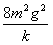⑩
练习册系列答案
相关题目
如图所示，一轻质细绳的下端系一质量为m的小球，绳的上端固定于O点．现用手将小球拉至水平位置（绳处于水平拉直状态），松手后小球由静止开始运动．在小球摆动过程中绳突然被拉断，绳断时与竖直方向的夹角为α．已知绳能承受的最大拉力为F，若想求出cosα的值，你有可能不会求解，但是你可以通过一定的物理分析，对下列结果的合理性做出判断．根据你的判断cosα值应为（ ）
如图所示，一轻质细绳的一端系质量m=0.01kg的小球，另一端系在光滑小环套在水平轴O上，O到小球的距离l=0.1m，小球跟水平面接触但无相互作用．在球的两侧等远处，分别竖立一固定挡板，两挡板平行并正对，相距S=2m，水平面上有一质量为M=0.01kg的小滑块，与水平面间的动摩擦因数μ=0.25，滑块和小球连线与档板面垂直，开始时，滑块从左档板处以V0=10m/s的初速度向小球方向运动，以后在与小球，档板每次碰撞时均不损失机械能，若不计空气阻力，（g取10m/s2） 求：
B.
C.
D.
B．
D．