Question

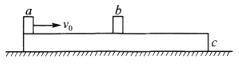
【题目】如图所示，在光滑的水平面上有一个静止的、足够长的木板，物块b静止在距离木板左端L=2.25m处，物块a以初速度v0=3m/s从左侧滑上木板，a、b均可视为质点。已知物块a、b与木板间的动摩擦因数均为=0.1两个木块与木板的质量均为m=1kg，a、b碰撞时间极短，碰后粘连在一起运动，滑动摩擦力等于最大静摩擦力，g取10m/s2。试求（结果可用分数表示）：

(1)a、b碰后瞬间的速度；

(2)最终状态时a、b距离c左端的距离。

Answer 1

【答案】（1）1.25m/s；（2）

【解析】

（1）a滑上c后水平方向受向左的滑动摩擦力，由牛顿第二定律得：

μmg=maa

代入数据解得

aa=1m/s2

若b、c相对静止，则b、c整体受a对它的向右的滑动摩擦力，由牛顿第二定律得

μmg=2ma0bc

代入数据解得

a0bc=0.5m/s2

由题意可知b与c间的动摩擦因数也为0.1，故b在c表面的最大加速度为

abm=μg=1m/s2

故bc可以保持相对静止，即

abc=0.5m/s2

则当ab将要相碰时满足

解得

t=1s（另一值舍掉）

此时a的速度

b和c的速度

a、b碰后粘连在一起运动，设共同速度为v，则由动量守恒

解得

v=1.25m/s

（2）当三者共速时速度为v′，则由动量守恒定律

由能量关系

解得

最终状态时a、b距离c左端的距离