题目内容
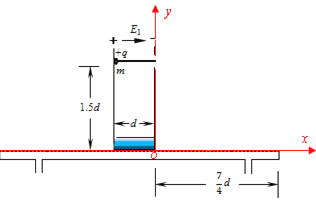
【题目】在如图所示的xoy坐标系中，一对间距为d的平行薄金属板竖直固定于绝缘底座上，底座置于光滑水平桌面的中间，极板右边与y轴重合，桌面与x轴重合，o点与桌面右边相距为
，一根长度也为d的光滑绝缘细杆水平穿过右极板上的小孔后固定在左极板上，杆离桌面高为1.5d，装置的总质量为3m．两板外存在垂直纸面向外、磁感应强度为B的匀强磁场和匀强电场（图中未画出），假设极板内、外的电磁场互不影响且不考虑边缘效应．有一个质量为m、电量为+q的小环（可视为质点）套在杆的左端，给极板充电，使板内有沿x正方向的稳恒电场时，释放小环，让其由静止向右滑动，离开小孔后便做匀速圆周运动，重力加速度取g。求：
（1）环离开小孔时的坐标值；
（2）板外的场强E2的大小和方向；
（3）讨论板内场强E1的取值范围，确定环打在桌面上的范围。
【答案】（1）环离开小孔时的坐标值是-
d；
（2）板外的场强E2的大小为
，方向沿y轴正方向；
（3）场强E1的取值范围为
，环打在桌面上的范围为
。
【解析】
（1）设在环离开小孔之前，环和底座各自移动的位移为x1、x2．由于板内小环与极板间的作用力是它们的内力，系统动量守恒，取向右为正方向，根据动量守恒定律，有：
mx1-3mx2=0①
而x1+x2=d②
①②解得：x1=
d ③
x2=d
环离开小孔时的坐标值为：xm=d-d=-d
（2）环离开小孔后便做匀速圆周运动，须
qE2=mg
解得：
，方向沿y轴正方向
（3）环打在桌面上的范围可画得如图所示，临界点为P、Q，则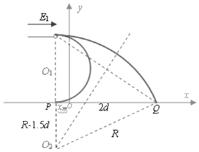
若环绕小圆运动，则R=0.75d ④
根据洛仑兹力提供向心力，有：
⑤
环在极板内做匀加速运动，设离开小孔时的速度为v，根据动能定理，有：
qE1x1=
mv2⑥
联立③④⑤⑥解得：
若环绕大圆运动，则R2=（R-1.5d）2+（2d）2
解得：R=0.48d⑦
联立③⑤⑥⑦解得：
故场强E1的取值范围为 ，环打在桌面上的范围为。
