题目内容
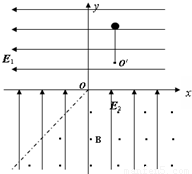
如图所示,在x轴上方有水平向左的匀强电场E1,在x轴下方有竖直向上的匀强电场E2,且E1=E2=5N/C,在图中虚线(虚线与y轴负方向成45°角)的右侧和x轴下方之间存在着垂直纸面向外的匀强磁场,磁感应强度B=2T.有一长L=5 m的不可伸长的轻绳一端固定在第一象限内的O'点,另一端拴有一质量M=0.1kg、带电量q=+0.2C的小球,小球可绕O'点在竖直平面内转动,OO'间距为L,与x轴正方向成45°角.先将小球放在O'正上方且绳恰好伸直的位置处由静止释放,当小球进入磁场前瞬间绳子绷断.重力加速度g取10m/s2.求:
m的不可伸长的轻绳一端固定在第一象限内的O'点,另一端拴有一质量M=0.1kg、带电量q=+0.2C的小球,小球可绕O'点在竖直平面内转动,OO'间距为L,与x轴正方向成45°角.先将小球放在O'正上方且绳恰好伸直的位置处由静止释放,当小球进入磁场前瞬间绳子绷断.重力加速度g取10m/s2.求:(1)小球刚进入磁场区域时的速度.
(2)细绳绷紧过程中对小球的弹力所做的功.
(3)小球从进入磁场到小球穿越磁场后第一次打在x轴上所用的时间及打在x轴上点的坐标.
【答案】分析:(1)小球由静止释放后,先沿电场力和重力的合力方向做匀加速直线运动,直到绳子绷直,绷直瞬间,小球沿绳子方向的速度突然减为零,以垂直于绳子方向的速度进入磁场.先由牛顿第二定律和运动学公式结合求出绳子绷紧前瞬间小球的速度,再将此速度分解得到垂直于绳子方向的分速度,由动能定理求解进入磁场时的速度.
(2)根据动能定理研究绳绷紧过程,求出细绳对小球的弹力所做的功.
(3)小球进入磁场后,由于qE2=Mg,小球做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律求出半径和周期,根据圆心角,求出小球在磁场中运动的时间.
解答:解:(1)小球先做匀加速直线运动,直到绳子绷直,设绳绷紧前瞬间速度为v,绳子刚绷紧后小球速度大小为v2,进入有磁场的区域时速度的大小为v3,
则 v2=2ax
而 F合=
又小球运动的位移为 x= L
L
绳子绷紧后:v2=vcos45°
由动能定理:Mg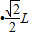 -qE1(L-
-qE1(L- )=
)=
联立解得:v3=10 m/s
m/s
(2)设细绳绷紧过程中对小球的弹力所做的功为W,根据动能定理得
W=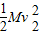 -
-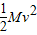
解得,W=-5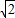 J
J
(3)小球进入磁场后,由于qE2=Mg,小球做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律得
qv3B=m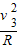
得 R= =
= ,T=
,T=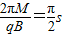
小球在运动半周后以v3出磁场,做匀速直线运动直到打到x轴上
匀速运动的时间t= ,小球从进入磁场到小球穿越磁场后第一次打在x轴上运动的总时间
,小球从进入磁场到小球穿越磁场后第一次打在x轴上运动的总时间
t总=t+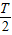 =
=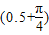 S=1.3s
S=1.3s
小球打到x轴上的位置坐标为(-10m,0)
答:
(1)小球刚进入磁场区域时的速度是10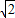 m/s.
m/s.
(2)细绳绷紧过程中对小球的弹力所做的功是-5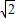 J.
J.
(3)球从进入磁场到小球穿越磁场后第一次打在x轴上所用的时间是1.3s,打在x轴上点的坐标为(-10m 0).
点评:本题小球在复合场中运动,分析受力情况,确定其运动情况是关键,与常规问题不同的地方是绳子绷紧瞬间小球的速度突变,沿绳子方向的速度立即减至零.
(2)根据动能定理研究绳绷紧过程,求出细绳对小球的弹力所做的功.
(3)小球进入磁场后,由于qE2=Mg,小球做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律求出半径和周期,根据圆心角,求出小球在磁场中运动的时间.
解答:解:(1)小球先做匀加速直线运动,直到绳子绷直,设绳绷紧前瞬间速度为v,绳子刚绷紧后小球速度大小为v2,进入有磁场的区域时速度的大小为v3,
则 v2=2ax

而 F合=

又小球运动的位移为 x=
 L
L 绳子绷紧后:v2=vcos45°
由动能定理:Mg
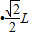 -qE1(L-
-qE1(L- )=
)=
联立解得:v3=10
 m/s
m/s (2)设细绳绷紧过程中对小球的弹力所做的功为W,根据动能定理得
W=
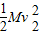 -
-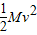
解得,W=-5
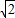 J
J(3)小球进入磁场后,由于qE2=Mg,小球做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律得
qv3B=m
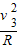
得 R=
 =
= ,T=
,T=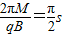
小球在运动半周后以v3出磁场,做匀速直线运动直到打到x轴上
匀速运动的时间t=
 ,小球从进入磁场到小球穿越磁场后第一次打在x轴上运动的总时间
,小球从进入磁场到小球穿越磁场后第一次打在x轴上运动的总时间t总=t+
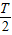 =
=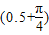 S=1.3s
S=1.3s小球打到x轴上的位置坐标为(-10m,0)
答:
(1)小球刚进入磁场区域时的速度是10
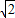 m/s.
m/s.(2)细绳绷紧过程中对小球的弹力所做的功是-5
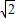 J.
J.(3)球从进入磁场到小球穿越磁场后第一次打在x轴上所用的时间是1.3s,打在x轴上点的坐标为(-10m 0).
点评:本题小球在复合场中运动,分析受力情况,确定其运动情况是关键,与常规问题不同的地方是绳子绷紧瞬间小球的速度突变,沿绳子方向的速度立即减至零.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,在x轴上方有匀强磁场B,一个质量为m,带电量为-q的粒子,以速度v从O点射入磁场,θ角已知,粒子重力不计,粒子在磁场中的运动时间为( )
如图所示,在x轴上方有匀强磁场B,一个质量为m,带电量为-q的粒子,以速度v从O点射入磁场,θ角已知,粒子重力不计,粒子在磁场中的运动时间为( ) 如图所示,在x轴上方有磁感应强度为B、方向垂直纸面向里的均匀磁场,x轴下方有电场为E、方向竖直向下的均匀电场,现有一质量为m、电量为q的粒子从y轴上某一点由静止开始释放,重力忽略不计,为使它能到达x轴上位置为x=L的一点Q,求:
如图所示,在x轴上方有磁感应强度为B、方向垂直纸面向里的均匀磁场,x轴下方有电场为E、方向竖直向下的均匀电场,现有一质量为m、电量为q的粒子从y轴上某一点由静止开始释放,重力忽略不计,为使它能到达x轴上位置为x=L的一点Q,求: 如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( )
如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( ) 如图所示,在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场.一个不计重力的带电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角,若粒子从x轴上的P点射出磁场,已知p点与O点的距离为a,则该粒子的比荷和所带电荷的正负是( )
如图所示,在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场.一个不计重力的带电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角,若粒子从x轴上的P点射出磁场,已知p点与O点的距离为a,则该粒子的比荷和所带电荷的正负是( )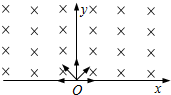 如图所示,在x轴上方(y≥0)存在着垂直于纸面向里的匀强磁场,磁感强度为B.在原点O有一离子源向x轴上方的各个方向发射出质量为m、电量为q的正离子,速率都为υ,对那些在xOy平面内运动的离子,在磁场中到达的最大x坐标和最大y坐标各是多少?
如图所示,在x轴上方(y≥0)存在着垂直于纸面向里的匀强磁场,磁感强度为B.在原点O有一离子源向x轴上方的各个方向发射出质量为m、电量为q的正离子,速率都为υ,对那些在xOy平面内运动的离子,在磁场中到达的最大x坐标和最大y坐标各是多少?