题目内容
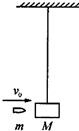 (2012?广东模拟)用不可伸长的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平地射向木块并停留在木块中,子弹初速度为v0,求:
(2012?广东模拟)用不可伸长的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平地射向木块并停留在木块中,子弹初速度为v0,求:(1)子弹射入木块瞬间子弹和木块的速度大小;
(2)子弹与木块上升的最大高度.
分析:(1)子弹射入木块过程,由于时间极短,子弹与木块间的内力远大于系统外力,故可由动量守恒定律列式求解;
(2)子弹和木块系统由于惯性继续上升,由于绳子的拉力不做功,只有重力做功,故系统机械能守恒,也可以运用动能定理求解.
(2)子弹和木块系统由于惯性继续上升,由于绳子的拉力不做功,只有重力做功,故系统机械能守恒,也可以运用动能定理求解.
解答:解:(1)子弹射入木块瞬间系统动量守恒
mv0=(M+m)v
解得 v=
.
即子弹射入木块瞬间子弹和木块的速度大小为
.
(2)子弹和木块一起上升过程中,只有重力做功,机械能守恒
(M+m)v2=(M+m)gh
解得 h=
.
即子弹与木块上升的最大高度为
.
mv0=(M+m)v
解得 v=
| mv0 |
| M+m |
即子弹射入木块瞬间子弹和木块的速度大小为
| mv0 |
| M+m |
(2)子弹和木块一起上升过程中,只有重力做功,机械能守恒
| 1 |
| 2 |
解得 h=
m2
| ||
| 2(M+m)2g |
即子弹与木块上升的最大高度为
m2
| ||
| 2(M+m)2g |
点评:子弹射木块是一种常见的物理模型,由于时间极短,内力远大于外力,故动量守恒;系统接下来的运动是摆动,也是一种常见的物理模型,机械能守恒,当然,能用机械能守恒定律解的题通常都能用动能定理解决!

练习册系列答案
相关题目
 (2012?广东模拟)一个平板小车置于光滑水平面上,其右端恰好和一个
(2012?广东模拟)一个平板小车置于光滑水平面上,其右端恰好和一个
 (2012?广东模拟)汽车从甲地由静止出发,沿平直的公路开到乙地刚好停止运动,其速度图象如图所示,在0-t1和t1-3t1两段时间内,汽车的( )
(2012?广东模拟)汽车从甲地由静止出发,沿平直的公路开到乙地刚好停止运动,其速度图象如图所示,在0-t1和t1-3t1两段时间内,汽车的( )