题目内容
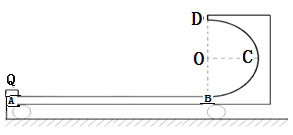
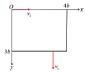
【题目】如图所示，在竖直平面内的矩形区域的坐标原点
处有一个带电微粒源，微粒发射方向均在
平面内。微粒质量均为
，带正电荷量均为
，重力加速度大小为
，（解题过程中可能用到
、
）.
(1)若整个矩形区域内存在与
轴方向平行的匀强电场，从点处射入一初速度沿轴正方向的微粒，发现其从坐标（
，）处垂直于轴方向射出矩形区域，求此微粒的初速度大小
以及电场强度的大小E；
(2)将电场方向改为竖直向上，再在整个矩形区域内加上垂直于平面向里的有界匀强磁场
。微粒源从点处发射的微粒速度大小
不等于)均相等，速度大小
介于
～
之间，入射方向在轴和
轴所夹的90°角范围内连续均匀分布。现测得在矩形区域内运动时间最长的微粒在进出该区域时速度方向改变了90°.请你分析说明微粒的运动特点并求入射微粒的速度大小.
【答案】（1）
；
（2）
【解析】
(1)粒子垂直进入电场做类平抛运动，结合水平方向和竖直方向上的运动规律，抓住等时性，结合牛顿第二定律和运动学公式求出电场强度的大小；
(2)根据洛伦兹力提供向心力求出粒子的半径从而求出速度.
(1)对沿x正方向入射的微粒，做类平抛运动.
x方向：
y方向：
联立可得：
沿x、y方向根据动量定理
解得电场强度
(2)将电场方向改为竖直向上后，电场力与重力平衡，微粒在洛伦兹力的作用下做匀速圆周运动.
设半径为r，由牛顿第二定律有：
由题设速度大小v2大小介于
之间，故微粒做匀速圆周运动的半径r大小介于3b~4b之间.
如图所示，微粒的运动轨迹与矩形相切于A点时，粒子的运动时间最长.微粒从O点进入矩形区域、从B点射出矩形区域.
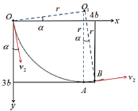
由题可得
.
设微粒入射方向与y轴夹角为α，根据几何关系可得：
联立消去α可解得：
可得：
练习册系列答案
相关题目
