题目内容
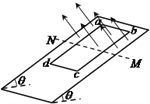
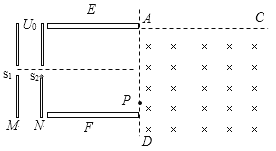
【题目】如图，金属板M、N板竖直平行放置，中心开有小孔，板间电压为
，E、F金属板水平平行放置，间距和板长均为d，其右侧区域有垂直纸面向里足够大的匀强磁场，磁场上AC边界与极板E在同一条直线上。现有一质量为m、电荷量为q的正电粒子，从极板M的中央小孔
处由静止释放，穿过小孔
后沿EF板间中轴线进入偏转电场，从AD边界上的P处离开偏转电场时速度方向与水平方向夹角为37°，已知sin37°=0.6，cos37°=0.8，忽略粒子重力及平行板间电场的边缘效应，求：
（1）粒子到达小孔时的速度
；
（2）P点与上极板的距离h；
（3）要使粒子进入磁场区域后不能从AC边射出，磁场磁感应强度的最小值。
【答案】（1）
（2）
（3）
【解析】试题分析：（1）粒子在加速电场中，根据动能定理可求出粒子到达小孔
时的速度；（2）进入偏转电场后，粒子做类平抛运动，根据类平抛运动的规律即可求P点与上极板的距离h；（3）根据几何关系求出半径R，根据运动的合成与分解原理求出进入磁场的速度，粒子在磁场中由洛伦兹力提供向心力，求出磁感应强度。
（1）粒子在加速电场中，根据动能定理得：
粒子到达小孔时的速度
（2）粒子离开偏转电场时，速度偏转角
，竖直方向速度
在偏转电场中，带电粒子做类平抛运动，则有：
，
则P点与上极板的距离
（3）要使得粒子不从AC边射出，R越大，B越小，R最大的临界条件就是圆周与AC边相切，由几何关系得
解得：
粒子进入磁场时速度
在磁场中，则有：
所加磁场的磁感应强度最小值为
练习册系列答案
相关题目
