Question

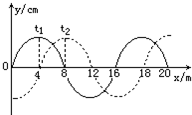如图所示，一列简谐横波在x轴上传播着，在t₁=0和t₂=0.05s的时刻，波的图象分别如图中的实线和虚线所示．这列波的波速可能是

v_右=80（4n+1）m/s或v_左=80（4n+3）m/s，（n=0，1，2，3，…）

．

Answer 1

分析：波的传播方向可能向右，也向左．根据波形的平移法，结合波的周期性，得出波传播的距离与波长的关系，求得传播距离的通项，再由v=

x

t

求解波速通项．

解答：解：若波向右传播：波传播的距离为x=（n+

1

4

）λ （m） （n=0，1，2，3，…）
则波速为v_右=

x

t

=

λ(4n+1)

4t

=

16(4n+1)

4×0.05

m/s=80（4n+1）m/s （n=0，1，2，3，…）
若波向右传播：波传播的距离为x=（n+

3

4

）λ （m） （n=0，1，2，3，…）
则波速为v_左=

x

t

=80（4n+3）m/s （n=0，1，2，3，…）
故答案为：v_右=80（4n+1）m/s或v_左=80（4n+3）m/s，（n=0，1，2，3，…）

点评：本题关键要抓住波的周期性和双向性，根据波形的平移法确定波传播距离与波长的关系．