题目内容
15.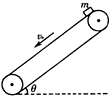 如图所示,足够长的传送带与水平面夹角为θ,以速度v0逆时针匀速转动.在传送带的上端轻轻放置一个质量为m的小木块,小木块与传送带间的动摩擦因数μ<tanθ,规定沿传送带向下为正方向,则图中能客观地反映小木块对传送带的摩擦力f随时间t变化关系的是( )
如图所示,足够长的传送带与水平面夹角为θ,以速度v0逆时针匀速转动.在传送带的上端轻轻放置一个质量为m的小木块,小木块与传送带间的动摩擦因数μ<tanθ,规定沿传送带向下为正方向,则图中能客观地反映小木块对传送带的摩擦力f随时间t变化关系的是( )| A. |  | B. | 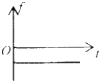 | C. | 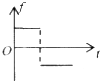 | D. | 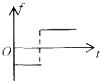 |
分析 要找出小木块速度随时间变化的关系,先要分析出初始状态物体的受力情况,本题中明显重力的分力与摩擦力均沿着斜面向下,且都是恒力,所以物体先沿斜面匀加速直线运动,有牛顿第二定律求出加速度a1;当小木块的速度与传送带速度相等时,由μ<tanθ知道木块继续沿传送带加速向下,但是此时摩擦力的方向沿斜面向上,从而即可求解.
解答 解:初状态时:重力的分力与摩擦力均沿着斜面向下,且都是恒力,所以物体先沿斜面匀加速直线运动,
由牛顿第二定律得:
加速度:a=$\frac{mgsinθ+μmgcosθ}{m}$=gsinθ+μgcosθ.
当小木块的速度与传送带速度相等时,由μ<tanθ知道木块继续沿传送带加速向下,
但是此时摩擦力的方向沿斜面向上,
而规定沿传送带向下为正方向,因此摩擦力方向先为正值,再为负值,故C正确,ABD错误;
故选:C.
点评 本题的关键1、物体的速度与传送带的速度相等时物体会继续加速下滑.2、小木块两段的加速度不一样大.是一道易错题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
6.一物体做匀加速直线运动,连续经过两端距离为64m的路程,第一段用时4s,第二段用时2s,则该物体的加速度是( )
| A. | $\frac{2}{3}$m/s2 | B. | $\frac{4}{3}$m/s2 | C. | $\frac{8}{9}$m/s2 | D. | $\frac{16}{3}$m/s2 |
20.物体做匀加速直线运动,加速度为2m/s2,那么( )
| A. | 在任意时间内,物体的末速度一定等于初速度的2倍 | |
| B. | 在任意时间内,物体的末速度一定比初速度大于2m/s | |
| C. | 在任意1s内,物体的末速度一定等于初速度的2倍 | |
| D. | 在任意1s内,物体的末速度一定比初速度大2m/s |
13.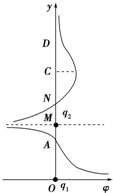 两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
 两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )| A. | q1与q2带同种电荷 | |
| B. | A、N两点的电场强度大小为零 | |
| C. | 从N点沿y轴正方向,电场强度大小先减小后增大 | |
| D. | 将一正点电荷从N点移到D点,电场力先做负功后做正功 |
14.在验证机械能守恒定律的实验中,要验证的是重锤重力势能的减少量等于它的动能的增加,以下步骤中仅是实验中的一部分,在这些步骤中多余的或错误的有( )
| A. | 把打点计时器固定在铁架台上,并用导线把它和低压直流电源连接起来 | |
| B. | 把纸带的一端固定在重锤上,另一端穿过打点计时器的限位孔,把重锤提升到一定的高度 | |
| C. | 接通电源,释放纸带 | |
| D. | 用秒表测出重锤下落的时间 |
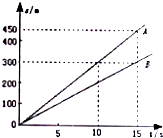 如图所示,A和B分别是甲乙两物体的s-t图象,则甲物体的速度v1=30m/s,乙物体的速度v2=15m/s,在t=15s时,甲、乙两物体相距150m.
如图所示,A和B分别是甲乙两物体的s-t图象,则甲物体的速度v1=30m/s,乙物体的速度v2=15m/s,在t=15s时,甲、乙两物体相距150m.