题目内容
质量为2000kg 额定功率为80kw 的汽车,在平直的公路上行驶时的最大速度为20m/s.若汽车从静止开始做匀加速直线运动,加速度大小为2m/s2,运动中的阻力不变,求:
(1)汽车所受阻力的大小;
(2)起初做匀加速运动的时间;
(3)3s末汽车的瞬时功率;
(4)汽车在匀加速过程中牵引力所做的功.
(1)汽车所受阻力的大小;
(2)起初做匀加速运动的时间;
(3)3s末汽车的瞬时功率;
(4)汽车在匀加速过程中牵引力所做的功.
分析:(1)当速度最大时,牵引力等于阻力,根据P=Fvm=fvm求出阻力的大小;
(2)根据牛顿第二定律求出牵引力的大小,根据P=Fv求出汽车匀加速直线运动的最大速度,再根据速度时间公式求出匀加速直线运动的时间;
(3)根据速度时间公式求出3s末的速度,再根据P=Fv求出汽车的瞬时功率;
(4)根据匀加速直线运动位移时间公式求出加速过程的位移,根据W=Fs求解牵引力做的功.
(2)根据牛顿第二定律求出牵引力的大小,根据P=Fv求出汽车匀加速直线运动的最大速度,再根据速度时间公式求出匀加速直线运动的时间;
(3)根据速度时间公式求出3s末的速度,再根据P=Fv求出汽车的瞬时功率;
(4)根据匀加速直线运动位移时间公式求出加速过程的位移,根据W=Fs求解牵引力做的功.
解答:解:(1)当速度最大时,F=f.
有P=fvm,则f=
=
N=4000N.
(2)根据牛顿第二定律有:F-f=ma.
则牵引力F=f+ma=4000+2×103×2N=8000N.
所以匀加速运动的最大速度为v=
=10m/s
匀加速直线运动的时间t=
=
=5s
(3)3s末时汽车还在匀加速运动状态
所以3s末汽车速度v2=at2=6m/s
所以3秒末汽车的瞬时功率P=Fv=8000×6W=48000W
(4)根据位移时间公式得:s=
at2=25m
则牵引力做的功W=Fs=200000 J
答:(1)汽车所受阻力的大小为4000N;
(2)起初做匀加速运动的时间为5s;
(3)3s末汽车的瞬时功率为48000W;
(4)汽车在匀加速过程中牵引力所做的功为200000J.
有P=fvm,则f=
| P |
| vm |
| 80000 |
| 20 |
(2)根据牛顿第二定律有:F-f=ma.
则牵引力F=f+ma=4000+2×103×2N=8000N.
所以匀加速运动的最大速度为v=
| P |
| F |
匀加速直线运动的时间t=
| v |
| a |
| 10 |
| 2 |
(3)3s末时汽车还在匀加速运动状态
所以3s末汽车速度v2=at2=6m/s
所以3秒末汽车的瞬时功率P=Fv=8000×6W=48000W
(4)根据位移时间公式得:s=
| 1 |
| 2 |
则牵引力做的功W=Fs=200000 J
答:(1)汽车所受阻力的大小为4000N;
(2)起初做匀加速运动的时间为5s;
(3)3s末汽车的瞬时功率为48000W;
(4)汽车在匀加速过程中牵引力所做的功为200000J.
点评:解决本题的关键知道发动机功率P=Fv,知道当速度达到最大时,牵引力等于阻力.以及知道以恒定加速度运动在整个过程中的运动情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

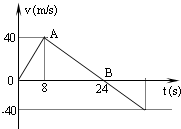 (2005?金山区二模)空间探测器从一星球表面竖直升空,已知探测器质量为2000kg(设为恒量),发动机推力为恒力.探测器升空后发动机因故障而突然关闭,如图所示为探测器从升空到落回星球表面的速度时间变化图象.试求探测器在星球表面达到的最大高度和发动机的推力.现有某同学的解法如下:
(2005?金山区二模)空间探测器从一星球表面竖直升空,已知探测器质量为2000kg(设为恒量),发动机推力为恒力.探测器升空后发动机因故障而突然关闭,如图所示为探测器从升空到落回星球表面的速度时间变化图象.试求探测器在星球表面达到的最大高度和发动机的推力.现有某同学的解法如下: