题目内容
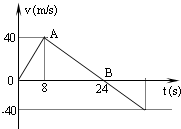 (2005?金山区二模)空间探测器从一星球表面竖直升空,已知探测器质量为2000kg(设为恒量),发动机推力为恒力.探测器升空后发动机因故障而突然关闭,如图所示为探测器从升空到落回星球表面的速度时间变化图象.试求探测器在星球表面达到的最大高度和发动机的推力.现有某同学的解法如下:
(2005?金山区二模)空间探测器从一星球表面竖直升空,已知探测器质量为2000kg(设为恒量),发动机推力为恒力.探测器升空后发动机因故障而突然关闭,如图所示为探测器从升空到落回星球表面的速度时间变化图象.试求探测器在星球表面达到的最大高度和发动机的推力.现有某同学的解法如下:由v-t图用计算三角形A0B面积的方法,来计算探测器在星球表面达到的最大高度h,h=
| 1 |
| 2 |
| 40-0 |
| 8 |
分析:探测器先向上做匀加速直线运动,发动机关闭后,先向上做匀减速直线运动,再返回做匀加速直线运动.根据图线围成的面积可以求出最大高度.在求解发动机推力时,题目中认为重力加速度为10m/s2,其实重力加速度不再是10m/s2,根据向上做匀减速直线运动可以求出重力加速度的大小.
解答:解:计算探测器在星球表面达到的最大高度是正确的,计算发动机的推力有误,应该这样来计算推力:
由v-t图算出探测器在星球上匀减速上升时的加速度g=
=2.5m/s2、
由牛顿第二定律,得到F-mg=ma,
则F=m(a+g)=2000×(5+2.5)=1.5×104N.
答:发动机的推力为1.5×104N.
由v-t图算出探测器在星球上匀减速上升时的加速度g=
| 40-0 |
| 24-8 |
由牛顿第二定律,得到F-mg=ma,
则F=m(a+g)=2000×(5+2.5)=1.5×104N.
答:发动机的推力为1.5×104N.
点评:本题是道易错题,很多同学思维定势,认为重力加速度与地球表面的重力加速度相等.所以解题时需细心.

练习册系列答案
相关题目
 (2005?金山区二模)如图所示,甲乙分别是两个电阻的I-U图象,则由图可知,甲电阻阻值为
(2005?金山区二模)如图所示,甲乙分别是两个电阻的I-U图象,则由图可知,甲电阻阻值为 (2005?金山区二模)矩形线圈abcd的边长ab=cd=40cm,bc=da=30cm,共有200匝,以300r/min的转速在磁感强度为0.2T的匀强磁场中绕垂直于磁场方向的中心轴OO′匀速转动,在t=0时刻处于图所示位置.此 线圈产生的感生电动势最大值e m=
(2005?金山区二模)矩形线圈abcd的边长ab=cd=40cm,bc=da=30cm,共有200匝,以300r/min的转速在磁感强度为0.2T的匀强磁场中绕垂直于磁场方向的中心轴OO′匀速转动,在t=0时刻处于图所示位置.此 线圈产生的感生电动势最大值e m=